Achievements
GROUNDWATER QUALITY PREDICTION OF A TAILINGS POND BY ARTIFICIAL NEURAL NETWORK
Pan Jianping, Kong Xianjing
State Key Laboratory of Coastal and Offshore Engineering,
Abstract: Wastewater from tailings pond, which contains H+、CN- and many kinds of metal ion, is the mostly polluting factors of groundwater at diggings. An investigation of groundwater pollution of tailings pond was carried out. Datum pertaining to various parameters such as pH and the contents metal ion were obtained from the investigation. Groundwater quality in the vicinity of tailings pond was analyzed, classified and predicted by a back-propagation network (BP) of improved arithmetic. The result discovers the mostly contamination and offers a scientific basis for fathering environment pollution of the tailings pond.
Key words: groundwater; tailings pond; artificial neural network; water quality prediction
1 Introduction
Groundwater pollution, from sources such as waste disposal sites, is a worldwide problem. Mining of mineral ores and disposal of resulting waste pose a significant risk to the groundwater [1-3]. The potential for mobility of toxic metals and acidity of Wastewater are the serious environmental problems involving the downstream water quality. Greater potential hazards are associated with the health impacts in the human population and changes in the natural environment through death of fauna and flora, loss of biodiversity and disturbance of ecosystem stability. Human health impacts through exposure to the contaminated groundwater arise due to the use of groundwater for domestic purposes. The migration of the pollution plume, albeit sometimes at a slow rate, will over time expose a greater number of the subsistence communities of the catchment to the contaminants in the pollution plume. Therefore, it is very important that the pollution of tailings wastewater is controlled and the quality of groundwater is classified and predicted.
Based on the analysis of the groundwater data collected during 14 years in this study, it is discovered that the density of contaminants presents nonlinearity with time. Therefore, the analysis and prediction of contaminants need to use the nonlinearity analysis method. Neural network model with adaptive and simulative capability can resolve complicated nonlinearity relation between evaluating genes and water quality grade and prediction [4-6]. In this paper, groundwater quality in the vicinity of a gold mine tailings pond is analyzed, classified and predicted by a back-propagation network (BP) of ameliorated arithmetic in this paper.
2 Sources of pollution
Gold mine occurs as bullion, quartz mine, in which the main chemical components is shown in table 1. Gold mine was first worked in 1976. The extraction of the ore produces mine drainage water, which is typically pollution source, and which has, in the past, found its way into the river systems. The waste rock and ore residues are pumped as ‘tailings’ to storage behind a specially constructed tailings dam. The common methods for disposal of tailings include disposal into a lagoon (natural or man-made), underwater or underground. Disposal into a lagoon is by far the most common method. Tailings are discharged at pulp densities typically in the range 30-40%. The tailings dam differ from the conventional water-retaining type structure in that the construction of a tailings dam is staged over the life of the impoundment by using upstream, downstream or a central line method of construction as schematically shown in Fig.1. The lifts of a tailings dam are scheduled to keep pace with the rising elevation of the tailings. The tailings dam in the gold mine was constructed using the upstream method.
Of all the issues related to disposal of tailings, there is perhaps none so environmentally sensitive or analytically complex as the seepage of liquid from the impoundment. Obviously with seepage occurring from a tailings impoundment, contaminants would become mobile via advective model transport resulting in the pollution of the underlying aquifer. It is reported that there was significant seepage from some tailings dam [7-8]. Several monitoring wells locate the downstream about
Table 1 The main chemical components of ore
SiO2/% | Fei2O3/% | MnO/% | Cu/% | Pb/% | Zn/% | Au/(g/t) | Ag/(g/t) |
74.22 | 7.69 | 1.17 | 0.078 | 0.082 | 0.254 | 7.2 | 33.8 |
Fig.1 Types of dam for tailings disposal
2 Framework and Design of BP Network
The back-propagation (BP) networks are the first and most commonly used, since they are characterized by the output error signal, which will be propagated backward to the input neurons from the successive layer to the preceding layer with strict learning schemes. BP networks are mainly applied in function approximation, pattern recognition, classific-
ation, and disposing relation between the inputs and outputs [9-12]. Designing of a BP network mainly includes the number of layers, the number of hidden nerve cells, the transfer function, parameters of network, etc.
2.1 Layers and hidden nerve cells
In order to establish the process model, we first need to describe how many layers and how many neurons per layer of the network are utilized in the network. The BP network is characterized by gaining possession of hidden layers. However, there is not a mature theory for deciding how many layers and hidden layers are adopted. Trial and error is still a common method [13]. A BP neural network without a hidden layer is adequate to describe the system of the linearized relationship between inputs and outputs. Generally, a BP neural network with a hidden layer is enough for most applications, and one with more hidden layers tends to make the network to complicated, a potential that results in more local minimums and causes lower convergence speeds and larger errors. Theoretically, BP with two hidden layers is enough to explain the complicated system with more general classic boundaries and has faster convergence speeds [9]. Commonly, the effect of adding the number of hidden layer is better than adding the number of network layer.
As analyzed in the section above, the number of the neurons in the input and output layers can be set 8 and 1, respectively. Generally, one hidden layer is enough to form the mapping between inputs and outputs. However, in order to describe the complicated nonlinear system, two hidden layers are used here, an arrangement that seems to have a better learning convergence speed and mapping relations. In the beginning, a small number of the neuron in the hidden layer is set to construct a lesser network. Training the network with examples, if the network can’t convergence or need too long training time, the process of training is stopped in time, then the neurons is added until the precision is enough and the training time is appropriate. In practical simulation, it is found that 17 neurons in the first hidden layer and 9 neurons in the second hidden layer are more efficient for better learning results. In other words, the designed 8×17×9×1 network structure is used here to perform the learning scheme (Fig.2).

Fig. 2 The sketch of BP network
2.2 Transfer function
The transfer function has several forms,such as the hyperbolic tangent, step, sigmoid function. However, the sigmoid function is the most common in practical application and is used here. The sigmoid
function has the capability of continuing magnification, can respond to arbitrary nonlinearity input/output. In order to transform input in (-¥, ¥) into output in (-1, 1), the transfer function in the first hidden layer is tan-sigmoid function, the one in the second hidden layer is log-sigmoid function, and the one in the output layer is pure-line function.
2.3 Parameters and initialization of network
⑴ Initial weight
The weight of each connecting line denotes the strength of the function between the two nodes. The magnitude of initial weight may affect the convergence speed, stability of network, etc.. In a general way, the small stochastic initial weight is adopted, for ensuring the network is not to be saturated by bigger weight and the output of every nerve cell is almost equal to zero after the initially weighted. Every nerve cell can adjust the weight at the peak value of sigmoid function. In this paper, NWTAN.M (a function) in the neural network toolbox is used to adjust the learning parameters W1、B
⑵ Expectation error
The expectation error decides training time, precision, number of hidden layer, and even reflects the approaching degree between the real output variable A and the objective vector T, namely, error square sum of network output. If the expectation error is too big, the training precision is not ensured. If the expectation error is too small, the training time is longer and may need to add the number of hidden layer. Considering there is a big difference among the groundwater quality indexes (the max difference reaches 106 times), the expectation error is assigned as 1.0e-7, especially ensuing the predicting precision of Cd is enough.
⑶ Learning speed
The variety of weight is affected by the learning speed of network. If there is a big learning speed, the network system may be instable, and even can’t converge. If there is a small learning speed, the training time is longer, but the error of network always can reach the expectation value and that it is avoided to fall into local minimum. Therefore, the small learning speed is commonly adopted by the users. The adaptive learning speed (Maxlinlr(P)) can automatically adjust the learning speed and ensure the network system safety and is adopted here.
2.4 Improved BP algorithm
Though the BP network is abroad applied, two major problems with BP algorithm include the slow convergence speed and the local minimum. A momentum factor is recommended to improve the performance of BP algorithm. The improved BP algorithm shortens the training time and adds the safety of neural network, which is incorporated into the function TRAINBPX.X in MATLAB toolbox.
3 Prediction and Classification of Groundwater Quality by BP
3.1 Prediction of groundwater quality
The application approaches of BP neural network include training weight, checking network, and prediction.
The contaminants in the pollution plume are mainly H+, CN-, and mental ion (Cu, Pb, Zn, Cd, Fe, Mn). Month mean for 12 years, in common 144 groups datum are used here as the training examples, and year mean is used as the objective vector (parts in table 2). Month mean for 2 years, in common 24 groups datum are used here as the testing examples (parts in table 3). The training weight and the value of the checking network in the simulation process are omitted here, and only the relation between time steps and the variety of error is shown in Fig.3.
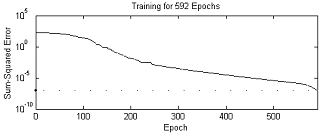
Fig.3 The variety of error with the steps
Table 2 Part training examples
Field testing time | Field testing indexes | |||||||
pH | CN— | Cu | Pb | Zn | Cd | Fe | Mn | |
| mg/l | |||||||
1991.01 | 6.490 | 0.432 | 0.300 | 0.070 | 0.820 | 0.006 | 0.908 | 7.473 |
1992.02 | 7.500 | 0.122 | 0.101 | 0.091 | 0.960 | 0.019 | 4.140 | 6.546 |
1993.03 | 6.860 | 0.018 | 0.108 | 0.070 | 2.520 | 0.052 | 0.630 | 4.536 |
1994.04 | 7.770 | 0.487 | 0.741 | 0.131 | 3.990 | 0.019 | 3.250 | 4.040 |
1995.05 | 6.760 | 0.087 | 0.337 | 0.177 | 1.780 | 0.078 | 1.076 | 4.518 |
1996.06 | 6.031 | 0.142 | 0.255 | 0.672 | 4.743 | 0.092 | 4.937 | 5.530 |
1997.07 | 6.830 | 0.075 | 0.091 | 0.323 | 3.790 | 0.101 | 0.167 | 3.010 |
1998.08 | 6.618 | 0.125 | 0.155 | 0.062 | 1.930 | 0.026 | 0.348 | 6.365 |
1999.09 | 7.234 | 0.062 | 0.147 | 0.057 | 0.701 | 0.015 | 0.637 | 3.329 |
2000.10 | 7.026 | 0.132 | 0.381 | 0.030 | 5.880 | 0.002 | 1.990 | 12.098 |
2001.11 | 7.158 | 0.038 | 0.204 | 0.355 | 2.533 | 0.047 | 0.863 | 12.185 |
2002.12 | 7.110 | 0.115 | 0.175 | 0.209 | 1.571 | 0.016 | 0.265 | 6.943 |
Objective vector | 6.9929 | 0.1259 | 0.2216 | 0.1510 | 3.0834 | 0.0285 | 5.8996 | 7.0380 |
Note: metal element calculated by the gross.
Table 3 Part testing examples and predicting results
Field testing time | Field testing indexes | |||||||
pH | CN— | Cu | Pb | Zn | Cd | Fe | Mn | |
| mg/l | |||||||
2003.07 | 7.010 | 0.036 | 0.044 | 0.116 | 2.648 | 0.019 | 0.421 | 5.880 |
2003.08 | 6.715 | 0.038 | 0.098 | 0.123 | 2.613 | 0.024 | 1.995 | 10.270 |
2003.09 | 6.947 | 0.033 | 0.115 | 0.104 | 2.524 | 0.024 | 0.364 | 7.382 |
2003.10 | 7.034 | 0.006 | 0.071 | 0.075 | 1.389 | 0.013 | 0.289 | 7.456 |
2003.11 | 7.078 | 0.075 | 0.095 | 0.137 | 1.735 | 0.020 | 0.207 | 8.440 |
2003.12 | 7.125 | 0.070 | 0.114 | 0.118 | 1.185 | 0.015 | 0.554 | 10.640 |
2004.01 | 7.200 | 0.129 | 0.113 | 0.150 | 1.446 | 0.017 | 0.334 | 4.067 |
2004.02 | 7.350 | 0.066 | 0.087 | 0.084 | 0.883 | 0.009 | 0.608 | 3.110 |
2004.03 | 7.216 | 0.032 | 0.055 | 0.131 | 1.483 | 0.019 | 0.475 | 4.601 |
2004.04 | 7.026 | 0.046 | 0.240 | 0.191 | 3.401 | 0.055 | 7.230 | 7.543 |
2004.05 | 7.126 | 0.040 | 0.134 | 0.214 | 3.283 | 0.035 | 13.22 | 7.929 |
2004.06 | 6.921 | 0.049 | 0.089 | 0.144 | 0.908 | 0.014 | 3.944 | 4.262 |
Real value | 7.156 | 0.0568 | 0.1179 | 0.1646 | 2.1364 | 0.0235 | 4.1850 | 6.1685 |
Forecasting value
| 7.1558 | 0.0568 | 0.1179 | 0.1646 | 2.1364 | 0.0235 | 4.1851 | 6.1686 |
3.2 Classification of groundwater quality
The aim of prediction of groundwater quality is to foresee the variety of water quality and make classification. The criterion of groundwater quality is GB/T 14848-93 (table 4) [14]. According to the analysis results above, the classification of groundwater quality is shown in table 5.
Table 4 The criterion of classification of groundwater(GB/T 14848-93)
Indexes | Unit | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
pH |
| 6.5~8.5 | 5.5~6.5,8.5~9 | <5.5, >9 | ||
CN— | mg/l | ≤0.001 | ≤0.01 | ≤0.05 | ≤0.1 | >0.1 |
Cu | mg/l | ≤0.01 | ≤0.05 | ≤1.0 | ≤1.5 | >1.5 |
Pb | mg/l | ≤0.005 | ≤0.01 | ≤0.05 | ≤0.1 | >0.1 |
Zn | mg/l | ≤0.05 | ≤0.5 | ≤1.0 | ≤5.0 | >5.0 |
Cd | mg/l | ≤0.0001 | ≤0.001 | ≤0.01 | ≤0.01 | >0.01 |
Fe | mg/l | ≤0.1 | ≤0.2 | ≤0.3 | ≤1.5 | >1.5 |
Mn | mg/l | ≤0.05 | ≤0.05 | ≤0.1 | ≤1.0 | >1.0 |
Table 5 The classified results of groundwater quality
Indexes | pH | CN— | Cu | Pb | Zn | Cd | Fe | Mn |
Class | Ⅱ | Ⅳ | Ⅲ | Ⅴ | Ⅳ | Ⅴ | Ⅴ | Ⅴ |
3.3 Results analysis and Remedial measures
⑴ Results analysis
Table 3 shows that the difference between real value and forecasting value is very small. The small error accounts for the BP network is stability and easy to converge. The value of pH is equal to 7.2, which indicates groundwater present neutral. Table 5 shows that only Cu belongs to Ⅲ, CN— and Zn belong to Ⅳ, and others (Pb, Cd, Fe,Mn) belong to Ⅴ. According to the criterion of classification of groundwater, Ⅳ and Ⅴ are polluted water, which can’t be used as the drinkable water source. As mentioned in the above, the groundwater in the diggings is badly contaminated and the people health may be endangered due to the pollutants entering into the river system.
⑵ Remedial measures
To control the high level of pollution of the
groundwater in the diggings, remedial measures are undertaken. The main remediation work is a cut-off trench is constructed in the downstream of tailings impoundment, and then the polluted water is pumped to send to the disposing plant. If the quantity of water pumped is large enough, the groundwater flow regime may be altered and a further expansion of the contaminated zone is avoided. Efficient monitoring strategies need to be developed for the more cost-effective remediation schemes can be offered.
4 Conclusions
In this paper, the BP network is improved to the learning algorithm and proved to be a better process modeling method. Based on the analysis of the testing datum for a tailings impoundment groundwater, a three layers improved BP network is constructed with the toolbox function in MATLAB, and then the groundwater quality is predicted and classified by the BP. The learning results for the groundwater quality reveal that the improved BP network can realize the mapping relations between inputs and outputs and the groundwater quality can be predicted with great accuracy. During simulation processes, it is also found that the new algorithm can reduce the local minimum to effectively obtain the global minimum and can accelerate the convergence speed of the learning processes helpfully. Thus, the improved BP network can be applied to future work on the prediction and classification of groundwater in the tailings pond. As shown in table 5, the metal pollutant of groundwater is very seriously in the diggings. A cut-off-trench is proposed to father the polluted groundwater. In addition, in order to provide the more cost-effective remediation schemes, efficient monitoring strategies need to be developed.
References
[1] C.J.von der Heyden, M.G. New. Groundwater pollution on the Zambian Copperbelt: deciphering the source and the risk. Science of the total environment, 2004, 327:17-30
[2] Marisol Manzano, Carlos Ayora, Cristina Domenech, etc.. The impact of the Aznalcollar mine tailing spill on groundwater [J]. The Science of the Total Environment, 1999, 242: 189-209
[3] R.S. Sharma, T.S. Al-Busaidi. Groundwater pollution due to a tailings dam [J]. Engineering Geology, 2001, 60:235-244
[4] Wang Ying, Sang Da-yong, Sun Lin-yan. The application of artificial neural network in Chinese environment forcast [J]. Environmental Science, 1997, 18(5): 81-83 (in Chinese)
[5] Guo Zhong-yang, Chen Zhong-yuan, Li Lv-qian. Artificial neural network and its application in regime prediction of groundwater quality [J]. Journal of east-china normal university (nature science), 2001, 3: 84-89 (in Chinese)
[6] Li Zuo-yong, Deng Xin-min. Application of artificial neural network to the assessment of water environment quality [J]. Environment Monitoring in
[7] Seedwel Ravengai, Richard Owen, David Love. Evaluation of seepage and acid generation potential from evaporation ponds, Iron Duke Pyrite Mine,
[8] G. Buselli, Kanglin, Lu. Groundwater contamination monitoring with multichannel electrical and electromagnetric methods [J]. Journal of Applied Geophysics, 2001, 48; 11-23
[9] Wen Xin, Zhou Lu, Wang Dan-li, etc.. Application and design of NN in MATLAB [M].
[10] Cong Shuang. The theory and application of NN in MATALAB toolbox [M].
[11] Dang Jian-wu. Technology and application of NN [M].
[12] Lou Shun-tian, Shi Yang. MATLAB-based system analysis and design of NN [M]. Xian: Press of university of electronic science and technology of xian, 1994,4 (in Chinese)
[13] H. Raman and N. Sunilkumar. Multivariate modeling of water resources time series using artificial neural networks [J]. Hydrologicial Sciences Journal, 1995,40(2): 145-163
[14] Bureau of National Technology Monitoring. Quality standard for groundwater [M]. 1




