SHAO Aijun, PENG Jianping, ZHANG Yongqiang

(Shijiazhuang University of Economics, Shijiazhuang, 050031, China)

Abstract: Hydrodynamic dispersion experiment was done with unsaturated silt loam. Depend on mass conservation law, the formulas to calculate coefficient of hydrodynamic dispersion was developed. According to the data of soil water and salt regime measured from the upright soil column, the coefficient of hydrodynamic dispersion was calculated, and the relation between hydrodynamic dispersion and average flow velocity in soil voids was built up. This approach has clear concept of physics, and the formulas are simple and applied.

Key words: Coefficient of hydrodynamic dispersion, Solute flux, Unsaturated soil.

1 Introduction

At present, the understanding of structure form in coefficient of hydrodynamic dispersion is not still unified (Wang yadong, Hu yuqi, 1992)^[1]. Theoretically, the coefficient of hydrodynamic dispersion D_sh is the sum of molecular diffusion coefficient D_s and the mechanical dispersion coefficient D_h. Generally, the molecular diffusion coefficient of solute in soil is only expressed for the function of soil water content, having nothing to do with the density of solute, and it usually is shown by empirical formula (Lei zhidong, Yang Shixiu, Xie Senchuan, 1988)^[2]. Kemper et al. (1966) using the empirical formula to show the molecular diffusion coefficient D_s is as following.

                                                             (1)

Where D_s is the molecular diffusion coefficient (cm²/min), D₀ is the diffusion coefficient of solute in the free water body, θis soil water content (cm³/cm³), a and b are the empirical constants.

According to the literature (Olsen and Kemper, 1968)^[3], while the soil water suction changes in the range of 0.3 ~ 15 atm, b =10 is more suitable in the above empirical formula, the changing range of value of a is 0.005 ~ 10.001 (silt loam to clay), the bigger the soil viscidity is, the smaller the value of a.

It is generally acknowledged, in one-dimensional flow, the mechanical dispersion coefficient D_h is in proportion to the one power of average flow velocity in soil voids (Bear, 1972) ^[4].

                                                                        (2)

Where D_h is the mechanical dispersion coefficient (cm²/min), v is the average porous flow velocity (cm/min), α is the dispersion degree (an empirical constant) (cm).

In the above foregoing, the dispersion coefficient D_sh stands for the sum of the molecular diffusion coefficient D_s and the mechanical dispersion coefficient D_h, that is,

                                               (3)

When the speed of convection is quite large, the function of the mechanical dispersion will greatly exceed the molecular diffusion, so only to need to consider the mechanical dispersion function in hydrodynamic dispersion. On the contrary, when the soil solution is static, the mechanical dispersion is completely inoperative, only leaving the molecular spreading. Generally speaking, there are molecular dispersion function and mechanical dispersion function at the same time in solute transfer in soil, but it is difficult to distinguish them, so the molecular diffusion and the mechanical dispersion are referred to as hydrodynamic dispersion. In practical application, some scholars express the coefficient of hydrodynamic dispersion as the exponential function of the coefficient of molecular diffusion form, such as Smiles and Philip (1978), Xie Senchuan, Yang Shixiu and Lei Zhidong (1988). They think longitude diffusion coefficient is not sensitive to the average flow velocity in soil voids, so D_sh can be alone treated as the function of the water content. However, from the literatures, many scholars express the coefficient of hydrodynamic dispersion as the linear function of the coefficient of mechanical dispersion form. They think that D_sh is in proportion to the one power of the average porous flow velocity. The coefficient of hydrodynamic dispersion is expressed as in the latter form in the paper ^[5]. The experimental method is the 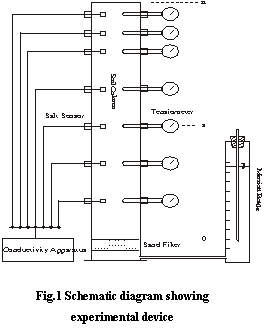indoors upright soil column.

2 Experimental Material and Method

The experimental soil was sampled from the estuary of the Changjiang River. The soil is silt loam, and the primitive salt content is 0.364g/kg, which is desalting soil. The soil sample used in the experiment through the natural air-drying is passed sieve mesh and mixed to well distributed. According to the actual dry density of the soil from the farmland, the soil column is filled. The degree of mineralization of supplying water in the experiment is 8g/L (close to the degree of mineralization of groundwater).

The soil column used is an upright soil column, which is made of the transparent plexiglas column, height 170cm, diameter 12.7cm. The side of the soil column is equipped with the salt sensor in order to monitor the soil salt content, and buried depth is 5, 15, 30, 45, 65, 105, 145cm, and tensiometer in the same depth to monitor the soil moisture content. Seal the bottom, open the top to evaporate. The experiment is done indoors. In order to be close to the natural environment condition, an infrared lamp is laid over the top of the column to imitate the sunlight. The bottom of soil column is equipped with Marriott bottle to control the water level and to monitor the consumption mass of water. The experiment lasted from August to October 1999, every 3 days once in the earlier and every 4 days once in the later got the observation record of soil electric conductivity, tension and the consumption mass of water. The experimental device is in Fig.1.

3 Calculation of Coefficient of Hydrodynamic Dispersion

To calculate the coefficient of hydrodynamic dispersion, firstly calculate the moisture flux, and then calculate the salt flux, finally determine the coefficient of hydrodynamic dispersion by the moisture flux and the salt flux.

3.1 Moisture flux

If both the mass of water that the solution supplied to the soil column through the bottom and the distribution of the profile water content at different moments were known, by water mass balance principle, the moisture flux q_z in any section z of the soil column can be expressed as follows.

                                                                                         (4)

That is

            (5)

Where q_z is the moisture flux in any section of depth z (cm/d), q₀ is the mass of inflow water mass from the bottom of the soil column (cm/d), θ is the volumetric water content (cm³/cm³), =t₂－t₁ is the time interval (d)。

The formula (5) is written in discrete form:

                                (6)

Where k is the number of time intervals.

3.2 Salt flux

If both the solute flux from the bottom of the soil column and the distributions of the sectional water content and of the solute density at different moments were known, by the mass conservation law, the solute flux J_z in any section depth of z can be got:

                                                                                 (7)

That is,

                                                                                 (8)

Where J_z is the so

lute flux in any section depth of z (g/cm²·d), J₀ is the solute flux in the bottom of the soil column (g/cm²·d), c is the density of soil solution (g/cm³), θis the volumetric water content (cm³/cm³), =t₂－t₁ is the time interval (d).

The equation (8) is written in dispers

ed form:

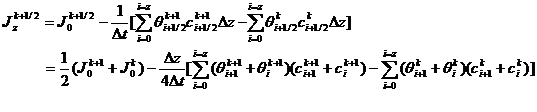              (9)

3.3 Coefficient of Hydrodynamic Dispersion

According to the hydrodynamic dispersion principle, solute flux is equal to the sum of the hydrodynamic dispersion flux and the convection flux, that is:

                                               (10)

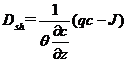                                              (11)

Where J is the solute flux (g/cm²·d), D_sh is the coefficient of hydrodynamic dispersion (cm²/d), c is the density of solute (g/cm³),θis the volumetric water content, =t₂-t₁ is the time interval (d).

The equation (11) is written in dispersed form:

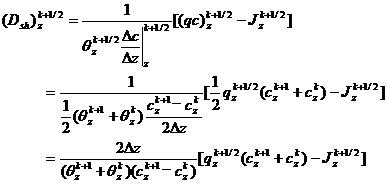                        (12)

Replacing the foregoing and into equation (12) can calculate the coefficient of hydrodynamic dispersion D_sh. If taking a series of section z, a series of D_sh can be calculated out Furthermore, D_sh and the corresponding average pore flow velocity v in soil voids can be fitted into empirical formula.

4 Results and Analysis

The experimental data of calculating the coefficient of hydrodynamic dispersion is shown in the following table (table 1).

Table 1 Data of hydrodynamic dispersion experiment

* the depth（cm）

Based on the experimental data of the above table, the coefficient of hydrodynamic dispersion can be calculated with the equation (12), in which the water content is calculated according to Van Genuchten model:

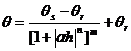                                             (13)

Where, the parameters according to the actually measured data for the water characteristic curve: θ_s is 0.432, θ_r is 0.01, is 0.006038, n is 1.9087501, m is 0.476097.

The conversion relation fitted by the experimental data between the electric conductivity and the salt content of soil is:

                                         (14)

Where s is the salt content of the soil (the salt mass of one unit mass dry soil (g/kg)), Ec is electric conductivity (mS/cm).

By calculating according to the experimental data, we has got the coefficient of hydrodynamic dispersion of the unsaturated slit loam.The coefficient value is in proportion to the average flow velocity in soil voids. The fitted curve is shown in Fig.2, and the correlate coefficient R=0.85, that is,

D_sh＝0.35v

Where D_sh is the coefficient of hydrodynamic dispersion (cm²/min), v is the average flow velocity in soil voids (cm/min).

In the test, as sensor and moisture tensiometer are arranged in large interval, it may influence the accuracy of the calculated result in some extent. Because solute transfer law is affected by a lot of factors, such as adsorption and desorption, the physics and chemical reaction, the original salt in soil, and so on, it is much more complicated than moisture movement. From the data of fitting figure, it can be found out that the fitting points are quite scattered, but the total linear tendency is still very clear. And the calculated values of the coefficient of hydrodynamic dispersion are quite close to the results calculated of other author, such as Yang Jinzhong, Huang Kangle, Zhang Yufang et. al. This approach is of clear physics concept and the calculated formula is simple and practical.