1 Introduction

The Groundwater Sustainable Yield is evolved from groundwater Safe Yield as the need of sustainable development arises since 20^th 90s ^[1~3]. It can be defined as the renewable yield that a groundwater system can provide, for an eternity, within its environmental carrying capacity ^[4].

Different from groundwater safe yield, the groundwater sustainable yield gives prominence to environmental factors, renewability and sustainability of groundwater systems ^[5].

Although the integrations of remote-control technique, tracing technique, GIS technique with water budget, numerical simulation etc used to assess groundwater sustainable yield have made significant progresses, there is still no perfect method to assess groundwater sustainable yield. More efforts need to accomplish the sustainable yield assessment.

On the other hand, with the proliferation of groundwater utilities, the global and regional evolutional rules of groundwater systems, of which equilibrium and stability is the basic and significant elements, have increasingly been the vital factors to groundwater sustainable use. At the same time, the anthropogenic disturbances especially from excess of groundwater abstraction have significantly complicated or even drastically damaged the groundwater systems. However, a customarily ignored fact is that groundwater budget is unequal to groundwater system equilibrium, groundwater system equilibrium is unequal to groundwater system stability, and stability of groundwater system is the prerequisite to assess groundwater sustainable yield. So the conventional ignorance and simplification of groundwater system's equilibrium and stability inevitably and increasingly affect and limit groundwater sustainable yield assessment.

Bredehoeft D. (1997, 2002), Sophocleous M. (1997, 2000), Frans.R.P. Kalf, (2005) proposed that numerical simulation is the best way to forecast groundwater equilibrium. But numerical simulation is effective to those natural or near natural systems with low entropies other than to those drastically disturbed groundwater systems with high entropies, in which equilibrium doesn't always mean stability, and of which the groundwater flow equation especially the terms of sinks and sources currently can't enough to characterize the interactions and functions with environment. On the other hand, even if the overall equation can well represent the evolutional dynamics of groundwater system, the stability analysis of equation with space derivatives is still difficult in term of systematic science.

To solve this issue, this article first distinguishes between the equilibrium and stability of today's groundwater system; and then sets up the evolutional model of groundwater system in terms of one-dimensional nonlinear differential equation, and by means of nonlinear dynamics further analyzes the equilibrium, stability, bifurcation, catastrophe of the groundwater system; finally, as an application, analyzes the stability and impose sustainable constraints on Taiyuan Groundwater Basin of Yellow River Catchment. This study will provide a novel methodology to study the evolutional rules and assess groundwater sustainable yield.

2 What is the Stability of Groundwater System

2.1 Open groundwater system

The groundwater system is an intricate four-spatio-temporal dimensional system, made up by independent entities, controlled by various interacting natural and human factors, and ceaselessly evolving ^[9~10].

The groundwater system is an important tache of water cycle and hydrological cycle, a vital subsystem of nature, and the result of natural evolution, selection, optimization, and has developed a pattern of effective substance and energy cycles. So, the groundwater system, under certain natural and human circumstances, can still maintain their structures and functions, exhibit certain self-organization and stability.

Most of groundwater system is open; it continuously exchanges substance, energy and information with exterior environmental systems. As the same as other substance system, the open groundwater system is non-balanced and nonlinear.

At the same time, the anthropogenic disturbances make the groundwater system far away from its original equilibrium state and cause system fluctuations, which will make the groundwater system have the features of the dissipative structure.

So, the features of modern groundwater system can be generalized as non-balanced, nonlinear and dissipative and nonlinear dynamics is the best methodology to study the stability of this kind.

2.2 The evolution of groundwater system

The ultimate reason for the groundwater system to evolve lies in its open and lies in the fact that it ceaselessly exchanges substances, energies and information with the environment.

Through the exchanges of substances, energies, and information, these environmental factors such as climate, hydrology, ecology, human activities etc change the sources and sinks of the groundwater system, and finally influence the dynamics of groundwater. The groundwater system, through the changes of water level, pressure, storage, temperature etc, self-adjusts its structures and functions, arouses the changes of system state and finally changes of rate and direction of evolution. These systematic changes may be obvious or unobvious, quantitative or qualitative, gradual or catastrophic.

At the same time, groundwater system, in return, by response of substances, energies and information, affects the exterior environment, which is the feedback to the exterior environments. However, when exceeding certain limits, the feedbacks will worsen the functions of environment, e.g. excessive groundwater extractions have widely caused subsidence, vegetation and desert, which had been the constraints to groundwater use.

For the near two decades, the characteristics of evolution of groundwater systems show that (1) it is mainly the anthropogenic disturbances that make the relationships between groundwater system and its environment more complicated, susceptible and unpredictable; (2) The rate, direction and behaviors of evolution of groundwater system may have changed greatly, or even deviate their natural equilibrium and stability; (3) Except for the groundwater system itself, the stability of the overall system of groundwater and environment is of more importance to groundwater sustainable use.

2.3 The stability of groundwater system

Under the nature or near nature circumstances, the connotation of Equilibrium is the same as that of Stability of groundwater system: (1) after a period time the open groundwater system achieves equilibrium and stable, and the state of which has the spatial and no temporal variables, (2) after a period time, the system can't finally reach equilibrium, will store or exhaust water. The un-balanced system with spatial as well as temporal variables is also unstable.

But currently when relatively great changes happening, the connotation of Stability of groundwater system is distinctly different from that of Equilibrium: (1) stability is the state of which, under certain exterior disturbances and even after deviating its equilibrium, the groundwater system can still restore to their original equilibrium; (2) instability is the state of which, even under tiny fluctuation, the groundwater system can not to restore their original equilibrium accompanied by qualitative change, or even die out. At this time, an equilibrious system may not be a stable system, stability is the high-class equilibrium.

The close system, in whatever original state, would end up with a kind of equilibrium state, a kind of static "dead" structure; while the unbalanced open system would end in a kind of stable ordinal state, which is a kind of dynamic "alive" structure.

The groundwater stability studies of this article include (1) the Lyapunov stability of the groundwater system caused by changes of system state variables, (2) the robust stability of groundwater system including bifurcation and catastrophe caused by changes of system governing variables.

3 Evolutional Model of One-Dimensional Nonlinear Groundwater System

3.1 Evolution model of one-dimensional nonlinear groundwater system

To effectively study the evolutional rules of groundwater system and solve the issue arisen from numerical simulation, this article, based on the storage dynamics of groundwater system, develops the evolutional model.

Assumed that by principal component analysis of groundwater system, the state and governing variables are selected as the following:

State variable X₁ called System State Index is the nondimensional configuration index of depression cone, which is the result of dynamics of groundwater.

Governing variable X₂ called Discharge Index is the nondimensional index of discharge resulted mainly from man's groundwater abstraction, which increases the sink potential of groundwater system.

Governing variable X₃ called Recharge Index is the nondimensional index of recharge, which increases the sink potential of groundwater system.

According to storage dynamics, the discharge index and the system state index of groundwater system constitute a positive feedback loop and the recharge index and the system state index of groundwater system constitute a negative feedback loop. The cause mode of groundwater system is shown in Fig.1.

Because the original configuration of the cone decides the dynamics of groundwater, including gradient, seep speed etc, the extending rate of the cone will increase with the extending of the cone, and the state index (X₁) is related with itself, which can be expressed as:

₍1)

At the same time, discharge index (X₂) increases and the recharge index (X₃) decreases the rate of state index, so the above (1) can be compensated as:

₍2)

But after the state index (X₁) increases to an extent, the state index itself would limit the increase of discharge index. This article uses the drying index (β) to express this kind of limitation, the evolution equation changes as:

₍3)

Namely,

₍4)

Let α=X₂-X₃, then the evolutional equation can also be expressed as:

₍5)

 

 

 

 

 

 

 

 

 

 

 

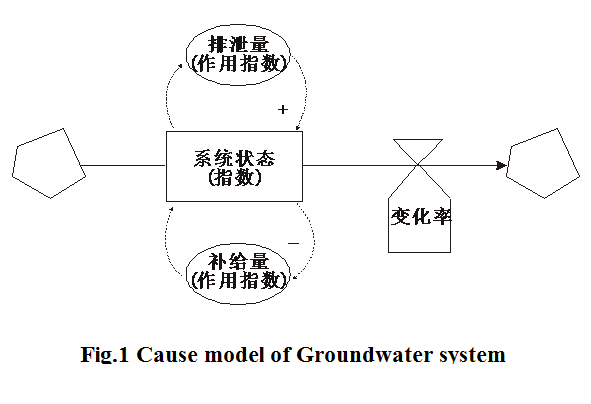
  Where α is decided by X2、X3, the drying index (β) represents the system’s compact attenuation related with abstraction, depth of aquifer, storage coefficient etc. With the increase of β, the limitation of β to discharge index also increases, the renewability of groundwater resources degrades.

So the evolutional model of groundwater system in terms of nonlinear difference equation is a one-dimensional, two-governing-variable, nonlinear dynamic system..

3.2 Stability analysis

According to the Lyapunov stability theory, let the right of (5) is zero:

（6）

Get the solutions of the stationary state of the groundwater system:

(7)

Assume that x₁ is the tiny disturbance near stationary state point, then:

X₁(t)=X_1，0+x₁，

Substitute the above for X₁(t) in (5), then:

，

get：

(8)

For , neglecting the quadratic term of tiny disturbance in (8), then:

（9）

That is the linearization to the nonlinear system, where ω=α-2βX_1，0.

(Ⅰ) To stationary state X_1，01=0

When, i.e. the discharge index less than the recharge index, then, according to the stability criterion of linear dynamic system, the system is gradually stable.

Inversely, when, i.e. the discharge index more than the recharge index, then, according to the stability criterion of linear dynamic system, the system is unstable.

(Ⅱ) To stationary state

From (9), get

So, when, i.e. the discharge index less than the recharge index, then, the system is unstable.

And, when, i.e. the discharge index more than the recharge index, then, the system is gradually stable.

The evolutional curve of groundwater system is shown in figure 2.

3.3 Bifurcation analysis

Assume that β is constant and the dynamic evolution equation can be expressed as:

（10）

The Jacobi matrix of the evolutional equation’s is:

（11）

Let

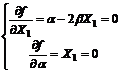
Then

X₁=0

α=0

So the bifurcation point is（X₁，α）=（0，0）

when α<0 and α>0, the equilibrium points of the state variable (X₁) respectively are X₁=0 and Y₁=α/β。At X₁=0, α<0 is stable and α>0 is unstable; At Y₁=α/β, α<0 is unstable and α>0 is stable. So when getting across the bifurcation point, the stability and instability is exchanged, while keeping the configuration of the phase trajectory unchanged. So the groundwater system belongs to striding critical bifurcation, as shown in figure 3.

3.4 Catastrophe analysis

The catastrophe of the groundwater system is the process that the groundwater system discontinuously changes from one equilibrium point to another.

According to the methodology of catastrophe theory:

Let, get the set of equilibrium points (M),

Get the Hessen matrix (H):

So the set of singular point (W) is

Remove X₁, get bifurcation set B:

So is the catastrophe point.

3.5 Relationship between evolutional curve and sustainable yield

To the one-dimensional dynamical groundwater system: (1) the equilibrium state X₁=0 can sustain stable only if α<0, the equilibrium state can sustain stable only if α>0; (2) In governing space of the model, α=0 is the bifurcation point and catastrophe point. So the equilibrium and stability of the system is governed by the symbol and value of α

β affects the magnitude of equilibrium state and the span of reaching stability. It is an important attribute and capacity parameter of the groundwater system itself, can balance the difference of input and output of the system.

Therefore, the system belongs to a kind of

 

uncertain stability. This study will mainly analyze the significance of robust stability dominated by exterior governing variables to sustainable yield.

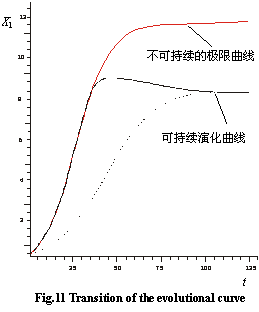
(1) α is the difference between discharge index and recharge index, when α>0, means discharge is bigger than recharge, the potential of sinks is more than that of sources, the magnitude of the equilibrium state increases with the increase of α (see fig. 4), and the time to reach equilibrium decreases.

On the other hand, the difference between discharge index and recharge index is limited. To a certain extent, the groundwater system will get into a state of still equilibrium, finally die out.

As shown in fig.4, Curve α₀ represents a kind of critical state; When α is more than α₀, the red curve in fig.4 demonstrates a kind of non-sustainable evolutional process, the groundwater system will die away; When α is less than α₀, the green evolutional curves in fig.4 represent a kind of living sustainable structure-function state.

So, when α>0, the balanced and stabilized state means that the system will inevitably exhaust a certain amount of storage and keep a certain size of depression cone. The accumulative changes of the groundwater system can be expressed in integral area of evolution curve (see fig. 5).

At Different equilibrious and stable state, the exhausted storage and left cones are also different, and maybe at the cost of the structure and functions of the environment.

Among the sustainable evolutional curves of groundwater system, each curve can meet different human needs and cause different influence on environment. And there must be one that can not only content peoples’ demands but minimize as possible the damage to the environment, which is the ideal optimal sustainable yield of groundwater.

The fig.4 and fig.5 can deeply enrich our comprehension to groundwater sustainable yield.

(2) When α<0, the discharge is less than recharge, the potentials of sink are also less than potentials of sources, the magnitude of equilibrium is X₁=0. But at present rate of abstractions, it is almost impossible to make α<0.

(3) As long as the system is not at the bifurcation or catastrophe point, i.e. α≠0, α can continuously change the direction, speed and course of evolution of the groundwater system, and continuously change the stability of the system.

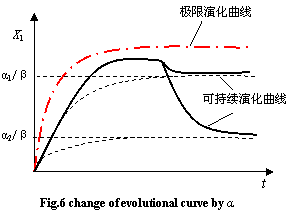
Because the abstraction of groundwater is controllable and adjustable, α can be reduced by adjusting the rate of abstraction so as to lower evolutional curve under the critical evolutional curve and escape the system from dying fate (see fig.6).

(4) The significance of this study still consists in the introduction of ecological and environmental

system, so as to set up th factors into the evolutional models of groundwater e dynamics of the overall groundwater system and environment.

4 Example Study

This article will take porous aquifer system of Taiyuan Basin, Yellow River as an example, study its equilibrium, stability and sustainable yield.

Before 20^th 70s, the basin groundwater system was nearly natural, the mid-deep confined aquifers were recharged by upper unconfined aquifers, the unconfined aquifers were mainly discharged by evaporation and withdrawl.

In recent years, mainly because of vast abstractions from the mid-deep confined aquifers; the basin groundwater system was severely altered and damaged. The system had no longer been a natural system but a human-nature-compound system. The shallow unconfined aquifers recharge mid-deep confined aquifer by penetration, and the withdrawal from the mid-deep aquifer has been main discharge of overall basin system. Now the shallow, mid and deep aquifers have come into being an integral dynamic system. The concept model of the Taiyuan basin groundwater system is shown in fig.7.

4.1 The evolutional model of basin groundwater system

It is because the Taiyuan basin groundwater system has been a man-nature-compound single layer aquifer with integral flow field that it can be viewed as a one dimensional nonlinear dynamic system.

After analyzing the time series of observed data of the basin groundwater system:

The state variable X₁ is the nondimensional configuration index of depression cone of the basin groundwater system;

The state variable X₂ is the nondimensional index of discharge of the basin groundwater system resulted mainly from man’s groundwater abstraction;

The state variable X₃ is the nondimensional recharge index of the basin groundwater system;

From the one dimensional nonlinear groundwater evolution model, the dynamic evolution equation of the basin groundwater system is

（12）

Let α=X₂-X₃, then the model can also be expressed:

（13）

The solution of the model is:

（14）

Assume that the 1965 as the original state, then

α=0.104

β=0.0084

k=2.8

Get:

（15）

From the former stability analysis, the basin groundwater system belongs uncertain stability, striding critical bifurcation, and exists one catastrophe point (α=0), the magnitude of stable state decided by α/β. Because of the deficiency of the observed data, this study assumes β=0.0083, the system reach equilibrious and stable at X₁=12.38.

4.2 Sustainable constraints and sustainable yield

Scenario 1: status in quo

At present the total groundwater abstraction of the basin groundwater system is 7.4×10⁹m³, the state index of the basin system is 8.46, the difference between discharge index and recharge index (α) is 0.104, β is 0.0084, the final stable state index is 12.38, which is the utmost drying state of the basin groundwater system, and the span of stabilization is about 35 years. The basin groundwater system is not in a sustainable state.

Scenario 2: status in quo as the targeted stable state

If taking the current state (X₁=8.46) as the targeted stable, according to the groundwater system dynamic equation (13) and its solution (14), the difference of discharge index and recharge index is 0.072, k=2.714, and the evolution model is

（5-5）

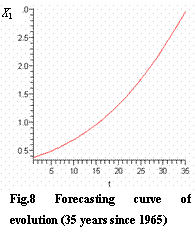
The evolution curves are shown in fig.8～10.

The system index will reach a new stability (X₁=8.371) after 100 years since 1965(see fig.9)

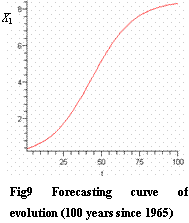
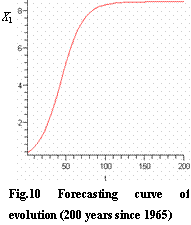
To avoid the basin groundwater system’s drying, lessen α to 0.072, the discharge index also should decrease 1.4 times of that in 1985 with the total

abstraction of 6.2×109m³, obtain the sustainable constraint of that scenario, which is expressed:

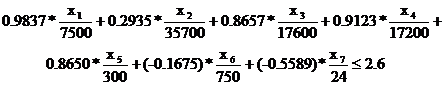
Where: X1 is the total groundwater abstraction;

X2 is the agricultural groundwater abstraction

X3 is the domestic groundwater abstraction;

X4 is the industrial groundwater abstraction;

X5 is the demographic total;

X6 is the rainfall;

X7 is the runoff volume;

And the sustainable evolution curve is shown in figure 12.

Scenario 3: optimal sustainable yield

To obtain the optimal sustainable yield, it should still integrate environmental factors into the evolutional model, should take into account of strategic target and decision action etc, and finally should consummate the sustainable constraints.

Scenario 4 discussion of parameters of α and β

If the condition permits, it should further discuss the evolution curve as α and β the changes simultaneously, which would improve r precision and reliability of assessment.

5 Conclusion

(1) Groundwater budget differ from groundwater equilibrium, and groundwater equilibrium differ from groundwater system stability. When budgeting or simulating the groundwater resource, the groundwater system equilibrium and system stability have always been neglected.

The groundwater system equilibrium and stability is the prerequisite of sustainable utilization. The best way to assess groundwater sustainable yield is to build groundwater dynamic evolutional model, analyze evolutional rules of equilibrium, stability etc, construct the groundwater sustainable constraints, and finally accomplish the assessment.

(2) Under the natural or near natural conditions, the equilibrium and stability is the same, the open groundwater system can reach its equilibrium between recharge and discharge, and the system also reaches its stable state. But anthropogenic disturbances have made the groundwater system deviate its original equilibrium and stability, the relationship between groundwater system and environment has been fragile, and the state of the groundwater system may be stable or unstable.

The connotation of stability can be summarized as (1) stability is the attribute of the groundwater system to restore to its own original equilibrium after the equilibrium of the groundwater system has deviated; (2) instability is the attribute of the groundwater system that can’t restore to its original equilibrium when the exterior disturbance drives the groundwater system to its critical point or with a tiny system fluctuation. At this time, an equilibrious system may not be a stable system, stability is the high-class equilibrium.

(4) The one-dimensional nonlinear groundwater system has two kinds of equilibrium state, it belongs to striding critical bifurcation, with a catastrophe.

With the increase of α, the magnitude of the system increases and the time to reach new equilibrium decreases. If the state index reaches a critical value, the system will die out.

If the system stabilizes at the state index of α/β, the system will finally exhaust certain groundwater storage and keep a certain size of depression cone, which may be at the cost certain environmental functions.

α can continuously change the course, direction and speed of evolution of groundwater, can continuously change the stability of the system. By adjusting the amount and strategy of groundwater abstractions, decrease α and make the system evolution curve restore to sustainable curve.

The utmost significance of this study lies that it provide a new methodology how to build human-ecology competing and cooperating groundwater model, how to analyzing the evolutional rules of the groundwater system, and analyzing the influence of system evolution to sustainable yield.

There is still not enough environmental data to construct prefect evolutional model of groundwater system, which restricts to develop the model.

(6) A little disturbance to a susceptible groundwater system today can easily damage the stability of the system..