Wang Xu, Yan E-chuan

(Faculty of Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China)

E-mail: summerwangxu@163.com

Abstract :After the Three Gorges reservoir is built, the reservoir water level will fluctuate between 175m and 145m because of the need of flood prevention and power generation. The periodical rise and descent of water level in high frequency and the influence of heavy rainfall will change the intrinsic geological circumstance and conditions greatly which may result in the instability of reservoir banks and slopes. Take a landslide locating in Zhongba reservoir bank as an example, according to the Three Gorges reservoir water level operation options, considering the influence of the practical rainfall intensity-duration course in the Three Gorges reservoir region, transient seepage influenced by the combination of the descending of reservoir water level from 175m to 145m and rainfall infiltration is calculated using the nonsteady fluid flow finite difference method ( FDM ) by which the changes of rainfall and reservoir level can be considered day by day. The transient nodal point head (infiltration lines) are then used for limit equilibrium analysis of landslide. The change laws of landslide stability are discussed under different calculation conditions. The results of stability analysis show that when the reservoir water level drawdown only, the coefficient of safety declines firstly, and then increases. There is a minimum safety coefficient when the reservoir level is at about 160m to 163m. In addition, when influenced by the combination of rainfall and reservoir water level drawdown, the safety coefficient of landslide will decrease all the time till the landslide revives, the critical reservoir water level is also at between 160m to 163m , which will need more attention in the treatment project of landslide in Three Gorges reservoir area.

Key words: rainfall, reservoir water level drawdown, nonsteady seepage, finite difference method, reservoir landslide, stability analysis

1 Introduction

With the rapid development of waterpower engineering, the study on the stability of reservoir bank arouse more and more recognition. And because of the universality, harmfulness, particularity of reservoir landslide, the study on the stability has a important significance in assuring the engineering construction operating successfully^[1].

Many facts have indicated that more than 95 percent landslides are associated with water directly^[2]. During the incubation and occurrence course of slope collapse, the effect of water is a critical extrinsic factor. Since the reservoir was in operation, under the new geological circumstance and conditions, the major factors which will result in the instability of reservoir banks and slopes are rainfall and the change of reservoir water level, especially the reservoir water level drawdown . Take Vajont reservoir which locates in Italy as an example, because of continuous rainfall and the abruptly rise and descent of reservoir water level induced by manmade operation factor, mass reservoir landslides occurred in 1963, and caused disastrous consequences. After the Three Gorges reservoir is built, the reservoir water level will fluctuate between 175m and 145m. The periodical rise and descent of reservoir water level in high frequency and the influence of rainfall infiltration will change the intrinsic geological circumstance and conditions obviously, including the changes of physico-mechanical property of soil, the changes of seepage forces caused by varying groundwater seepage filed and so on, which maybe results in the instability of reservoir banks slopes and reviving of landslide. So the study on the influence by the combination of rainfall infiltration and reservoir water level drawdown on the stability of reservoir landslides is of great importance in current landslide research field, and the reasonable determination of groundwater seepage field affected by this combination in landslides is critical in accessing the stability of reservoir landslides.

At present, in the stability evaluation and treatment design of landslides in Three Gorges reservoir area, when considering the influence of groundwater on the stability of landsides, the determination of phreatic surface (infiltration line) lacks of theoretical basis ^[3], or confirm a line factitiously by experiences, or adopt steady seepage calculation methods which consider the reservoir level descends suddenly，and these may make engineering treatment unsafety. In fact, when rainfall and reservoir water level descends, the groundwater seepage filed inside the landslide is a dynamic nonsteady seepage field which correlates some factors such as drawdown velocities of reservoir water level, rainfall intensity-duration and filtration coefficient and so on. So all these factors should be considered in the stability analysis of reservoir landslide, and then groundwater nonsteady seepage analysis method is adopted to gain practical groundwater level (phreatic surface), by which the seepage forces and the weakened area of soil’s parameters can be ascertained.

There for, a landslide which locates in Zhongba reservoir bank, ZiGui county in Three Gorges reservoir is taken as an example, transient seepage field influenced by the combination of the descending of reservoir water level from 175m to 145m and rainfall infiltration is calculated though establishing nonsteady fluid flow finite difference equation by which the rainfall and the change of reservoir level can be considered day by day, then the distributions of transient infiltration lines are obtained, and mathematic model for stability analysis of landslide is established. Transient safety factors are gained by using limit equilibrium analyses of landslide, the change laws of landslide stability are also discussed under different calculation conditions.

2 Basic Geological Characteristics of

Landslide

The Zongba landslide is a old accumulation landslide, which forms after the second terrace formed. Its plane shape looks like sector and chair-form at rear border is explicit. The slippage is about 80 meters. The front mass glides and overlays over the second terrace, and the upper clay layers of the third and forth terraces in middle-rear part are participating in gliding. The landslide is 139m to 215m in height, 67×10⁴ m³ in bulk, covering an area of 8×10⁴m² and its main slide direction is NE 65°. Hydrogeologic conditions are simple in this area, the groundwater is mainly supplied by rainfall infiltration and the pond locating in the area. And because of the intimate hydraulic association between the groundwater and the reservoir water, the groundwater level is affected by the fluctuation of reservoir water level.

Sliding mass（Q^del）which is dualistic structure mainly consist of silty clay, silty clay containing broken stone, broken stone soil and block stone, and the bottom are silty clay containing pebble and sandy clay. Its thickness is about from 4m to 19m, and the average is 8.0m. The sliding mass presents medium-weak permeable characteristic. Sliding band soil mainly consist of silty clay containing pebble, containing broken stone in local parts. It is 0.2m to 1m in thickness and presents medium-weak permeable characteristic. The lithologic characters of sliding-bed are mainly colluvium and slope materials（Q^col+dl）, parts are alluvium and diluvium (Q^pl+al). Silty clay containing pebble, sandy clay and pebble layer are included. The sliding bed is 7m to 16.44m in thickness, and is medium permeable. Base rock（J_3p）which is composed of siltpelite and arkose-quartzite locates in bottommost part. It is 17m to 30.43m in depth, and has a tight perviousness. Base rock surface approaching the river is formed by the erosion of old river-bed, and the figure is irregular. the shape of slide plane is also irregular, steep in middle-rear part, and gentle in front part.

Except geological structure, lithologic characters and the landform, hydrogeologic conditions in landslide area are also important factors affecting the stability of the landslide. Although the simple rainfall infiltration would affect the stability of the landslide, such as uplifting the groundwater level, increasing the seepage forces forward, weakening strength parameters and so on. But the Zhongba landslide had undergone the rainstorm after its formation, and is apt to be stable. So the simple rainfall infiltration will not cause the landslide reviving again. However, after the Three Gorges reservoir was built, with the physical and chemical influence of the water, the shear intensity of both sliding mass and sliding band will decrease, especially when the reservoir water level drawdown, the groundwater inside sliding mass will discharge. If the reservoir water level drawdown velocity is too fast, the inside-water cannot discharge, seepage forces of nonsteady seepage then increase, additionally the influence of rainfall infiltration, the state of the landslide stability will be deteriorated. So, the influence by the combination of reservoir water level drawdown and rainfall should be taken into account in the stability evaluation of Zhongba landslide.

3 Nonsteady Seepage Simulation

inside Landslide

3.1 Basic principle of unsteady groundwater seepage analysis

According to the study on the hydrogeologic conditions of Zhongba landslide, the influence by combination of reservoir water level drawdown and rainfall on the stability of reservoir landslides should be considered. At the moment, the groundwater seepage field must be settled by nonsteady seepage analytic method because the seepage is unsteady.. When taking the head H as dependent variable of the control equation, the differential equation (Boussinesq equation) ^[4] which suits for nonsteady motion of the phreatic water is:

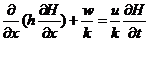（1）

If the step size △x in x direction is chosed by different spacing interval, using difference coefficient instead of differential quotient, in heterogeneous rock and soil stratum, equation (1) can be replaced by following equation (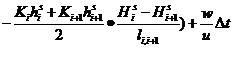2):

（2）

Remarks: S represents the start of a time-interval △t; S+1 represents the end of a time-interval △t; h_i-1, h_i，h_i+1 and H_i-1, H_i，H_i+1 represents separately the aquifar thickness and water head of profile i-1，i，i+1; l_i-1,i，l_i,i+1 represents separately the distance between profile i-1 and i，i and i+1; W represents infiltration or evaporation capacity in unit area during unit time; u represents water yield or deficiency of saturation; K_i represents the average permeability coefficient of profile i which is a weighted average calculated by thickness of different soil layers.

According the above principle, Seepage procedure which can consider the real-time change of rainfall intensity-duration and reservoir water level drawdown is compiled by FORTRAN language.

3.2 Some key techniques in implementation of calculation procedure

(1) Disposing of rainfall boundary and reservoir fluctuation boundary

Considering the influence by change of the reservoir water level on the seepage field, we present the change of reservoir water level as boundary condition using known head nodal points form. In order to consider the change situation of the groundwater level along with the change of time, the relationship curve between the elevation of reservoir water level on sloping surface and the time (given by discrete points form) and possible known head nodal points need to be given. Then, in the calculation procedure, the reservoir water level elevation at the calculating time is calculated using linear interpolation by time. Also, for the curve which expresses the change of rainfall intensity-duration along with the change of time, the data is input by discrete points form. and in calculation procedure, we also use linear interpolation by time to calculate the rainfall intensity at the calculating time. If the rainfall intensity exceeds the permeability coefficient of soil, the redundant rainfall capacity will not reckoned in seepage calculation.

(2) The time step size problem in calculation

Because in the calculating course of explicit finite difference, time step size directly affects the convergence and calculation accuracy. So, it is necessary to choose a reasonable time step size. But, considering so great many influential factors such as space time size, aquifer thickness, permeability coefficient, we hardly confirm the best reasonable time step size before calculation. And with the changes of the groundwater level and the average permeability coefficients of the section, the reasonable time step size also continuously changes. Therefore, in order to ensure the convergence, we adopt self-correcting time step size method in procedure to solve the problem.

3.3 Seepage calculation model, parameters and boundary conditions

According the engineering geological characteristics of Zhongba landslide, choosing 9-9’ longitudinal profile, and taking the range influenced by the reservoir water level drawdown and rainfall infiltration into account, the groundwater seepage calculation area is confirmed, and then is divided into 37 sections, spacing interval between adjacent sections (space step size) is 10m, the section 1 to 37 are as shown in Figure.1. We choose the time which is cost by reservoir water-level drawdown from 175m to 145m and one month after reservoir water level stops drawdown (considering hysteresis quality of groundwater movement) as the calculation time.

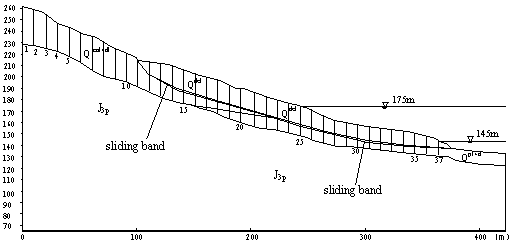
Figure.1 Discrete FDM model for seepage caculation

The hydrogeologic boundary conditions are as follows: 175m to 145m is the variation boundary of reservoir water level by stages; all the ground is supply boundary of rainfall infiltrating; the value of the boundary point is directly defined by the boundary conditions; seepage calculation area contains all sections, including the variation boundary of reservoir water level and supply boundary of rainfall infiltrating. Left boundary (in section 1) is constant flow amount recharge boundary, the recharge amount is steady seepage discharge per unit width which is calculated by the observed groundwater level during present rainless period. The permeability coefficient of base rock（J_3p）is about 0.034m per day, so it can be considered as watertight boundary.

Hydrogeologic parameters for calculation is listed in Table 1.

3.4 Calculation schedules

Table 1 Hydrogeologic parameters for calculation

According to the Three Gorges reservoir water level operation options, when reservoir water level descends from 175m to 145m, the descending velocities are about 0.6 to 2 m per day, less than 3 m per day, then the drawdown velocities are confirmed in two situations: 1 m/d and 2m/d separately. When confirming rainfall boundary model, considering that rainstorm and continues rain are two factors affecting the stability of landslide in Gorges reservoir area, so the two rainfall types are all adopted in a designed rainfall intensity-duration course. Based on historical rainfall data in ZiGui county in Three Gorges reservoir, the continues rain intensity which is 10 mm per day and rainstorm intensity which is 100 mm per day are confirmed by using the extreme distribution, and the occurrence probability of rainstorm is 5 days in 20 years. The rainfall intensity in a day is equicohesive. Fig 2 shows a designed rainfall intensity-duration curve while reservoir water level drawdown (when t=0d, water level descend starts) in terms of historical rainfall data.

Fig.2 Rainfall intensity-duration curve while reservoir water level drawdown

Calculation schedules are as follows:

(1) no rainfall, reservoir water level descends from 175m to 145m, and the drawdown velocity is 1m/d and 2m/d separately.

(2) combination of rainfall and reservoir water level drawdown, the reservoir water level descending velocity is 1m/d and 2m/d separately, and continues rain intensity is 10 mm /d, rainstorm intensity is 100 mm /d.

3.5 Calculation process

Initial seepage field, of which the head distributions can be solved by steady seepage method, is the basis of nonsteady seepage calculation. Firstly, use the observed ground -water level during present rainless period to calculate the steady seepage discharge per unit width. Because the quantity of rainfall is very little during rainless period, the calculated steady seepage discharge value per unit width is the seepage recharge value from upper profile. Then the discharge is used to calculate the steady groundwater level when reservoir water level rises from present water level (139m) to 175m, which is considered as the initial groundwater level for other calculation schedules. In every calculation time-interval, take the head distribution in the end of upper time-interval as the initial value for calculation. In addition, when reservoir water level descends, take the head value in the end of descending time-interval as reservoir water level fluctuation boundary value.

3.6 Analysis of calculation results

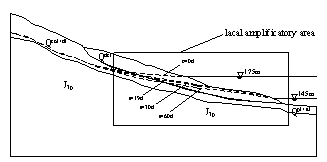(a) infiltration lines when v=1m/d，t=0,19,30,60d

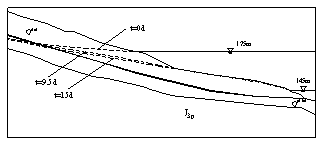(b) infiltration lines (local amplify) when v=1m/d， t=0,19,30,60d

(c) infiltration lines (local amplify) when v=2m/d， t=0,9.5,15d

Figure.3 Infiltration lines for different drawdown velocities (no rainfall)

Figure.4 Infiltration lines when v=1m/d，t=0,19,30d (rainfall)

(1) Change laws of transient seepage for different drawdown velocities

Change laws of infiltration lines for different drawdown velocities are shown in Fig.3. When the reservoir water level descends to a same level, the drawdown velocity is more faster, the infiltration line is more steeper, and the hydraulic gradient is more bigger.

(2) The influence of rainfall on seepage field

When drawdown velocity is 1 m/d and rainfall occurs simultaneously, the infiltration lines at some time are shown in Fig.4. Compared with Fig.3(a), it is clear that infiltration lines uplift obviously because of rainfall infiltration.

(3) It can be gained from Fig.3 (b) that after reservoir water level reach steady state (t=30d), namely the reservoir water level is at 145m and will not descend any more, because of the hysteresis quality of groundwater movement, the groundwater level will continue to decrease till reach a steady seepage state which is helpful for the stability of landslide. The results conform to the reality.

(4) The calculation course still indicates that there are some bleeding areas forming on local sloping surface, and it is harmful for stability of surficial soil. This phenomenon is variant in different calculation schedules and its occurrence mainly depends on sectional inflow and outflow amounts of phreatic water inside that slope body which are associated with hydraulic gradient, aquifar thickness and rainfall capacity.

4 Evaluation of Landslide Stability under Nonsteady Seepage Condition

The distributions of nodal point heads of transient seepage at every time in landslide which are calculated by FDM are then used for limit equilibrium analysis under different calculation conditions. One of limit equilibrium analysis methods named remained slip force method is adopted, and the method assumes that there are only remained forces existing between slips, and the direction of remained forces confirms to the direction of slide surface of upper slip. On slide surface, effective normal stress and tangential stress conform to Mohr-Coulomb criteria. The loads considered applying on slips are mainly gravity force itself, anti-gliding force, seepage force and uplift pressure which are caused by groundwater. Weakened effects of groundwater on soil’s parameters is also considered.

Based on large quantities of indoor-outdoor experiments, associating with engineering geology analogical method, we take different strength parameters corresponding to different sections of sliding band as shown in Table 2, and unit weight parameters of sliding mass are summarized in Table 3.

Table 2 strength parameters of sliding band

Table 3 unit weight parameters of sliding mass

4.1 Influence of different reservoir water level drawdown velocities on landslide stability

According to the seepage and stability analysis of Zhongba landslide, when the reservoir water level descends to a same level, the drawdown velocity is more faster, the safety coefficient of landslide is smaller. Moreover, the drawdown velocity is more faster, the time spending on reaching the minimum safety coefficient is less. For example, when drawdown velocity is 1m per day, it will take 19 days for reservoir water level to descend from 175m to 156m, and the safety coefficient of landslide falls down to 1.141. And when drawdown velocity is 2m per day, the time needed for reservoir water level descending from 175m to 156m are 9.5 days, and the safety coefficient of landslide is 1.124 at that time.

It is shown in Fig.5 that the coefficient of safety declines firstly, and then increases when the reservoir water level drawdown only, And there is a minimum safety coefficient when the reservoir level is at between 160m and 163m. After reservoir water level reaches steady state, namely the reservoir water level is at 145m and will not descend any more, because of the hysteresis quality of groundwater movement, the safety coefficient of landslide will continue to increase till reach a steady value when the seepage is steady.

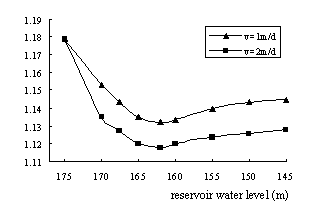
Fig.5 Relationship between stability of landslide and drawdown velocities of reservoir water level

4.2 Effects of rainfall on stability of landslide

According to historical rainfall data in ZiGui county in Three Gorges reservoir, both continues rain and rainstorm infiltration are considered in a designed rainfall intensity -duration course. Continues rain intensity is 10 mm/d, and rainstorm intensity is 100 mm/d. The stability of landslide is calculated in two combination situations: (1) reservoir water level drawdown velocity is 1m/d, and rainfall happens at the same time; (2) drawdown velocity is 2m /d, and rainfall happens at the same time. The results are showed in Fig.6. Rainfall infiltration will uplift the groundwater level and augment the values of seepage forces, so with the increasing of rainfall intensity, the stability of landslide decreases. As showed in Fig.6, both the reservoir water level elevation from 170m~165m when drawdown velocity is 1m/d and the reservoir water level elevation from 165m~155m when drawdown velocity is 2m/d are corresponding to the rainstorm time in rainfall course, and during this time, the stability of landslide decreases greatly. We can also see that along with the rainfall proceeding, the coefficient of safety decreases all the time.

At the same time, some conclusions can be obtained through analyzing Fig.5 and Fig.6. In no rainfall situation, whether the drawdown velocity is 1 m per day or 2 m per day, the landslide is steady. But under the combination of rainfall infiltration and reservoir water level drawdown conditions, the landslide will loss of stability when the water level has descended 12 to 15m, the critical reservoir water level is also at between 160m to 163m. Of course, the critical reservoir water level changes when the rainstorm time fluctuates during rainfall course.

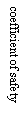
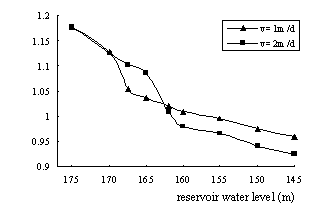
Fig.6 Effects of rainfall on stability of landslide

5 Conclusions

(1) Because when influenced by the combination of practical rainfall intensity -duration course and reservoir level drawdown day by day, the groundwater seepage filed is a dynamic nonsteady seepage field, and there are some difficulties in studying the seepage model at present. But the real-time influence by the combination can be considered using nonsteady seepage theory. Through the nonsteady fluid flow finite difference simulation, the transient nodal point heads (infiltration lines) at every time can be obtained, then transient safety coefficients of landslide are calculated by limit equilibrium analysis. This method put forward in this paper conforms to the real operation of Three Gorges reservoir more than other methods such as steady seepage calculation method.

(2) when reservoir water level drawdown only, the coefficient of safety declines firstly, and then increases. There is a critical reservoir level while safety coefficient of landslide is minimum. Through the analysis of Zhongba landslide, the critical reservoir level is at about 160m to 163m.

(3) when influenced by the combination of rainfall infiltration and reservoir water level drawdown, the safety coefficient of landslide will decrease all the time till the landslide revives, the critical reservoir water level is also at between 160m to 163m , which will need more attention in the treatment project of landslide in Three Gorges reservoir area.

(4) The drawdown velocity and rainfall intensity are two factors affecting the stability of landslide. With the increasing of rainfall intensity, the stability of landslide decreases. And when the reservoir water level descends to a same level, the drawdown velocity is more faster, the safety coefficient is smaller. Moreover, the drawdown velocity is more faster, the time spending on reaching the minimum safety coefficient is less.