Evolutional Rules of Regional Groundwater System
QUANTITATIVE ANALYSIS OF WATER HEAD LAG EFFECT IN CONFINED AQUIFER
Lu yudong1,2) Li peicheng1)
1)College of environmental sciences and engineering ,Chang’an University, Xi’an 710054,China;
2) College of resources and environmental sceiences, Chongqing
University, 400044,
Abstract: There
are stagnant flow in confined aquifer during pumping test. In this paper,
inertial equation is derived by applying contiguous media dynamics theory.
Ground water transport equation, which contain acceleration term, is a
attenuation wave equation, and include time parameter representing by ![]() . The spread velocity of water head is
function of catchment rate, and water and solid media is more compressive , the
spread velocity is more little. In fact ,there is a lag time between the water
level change of well in confined aquifer and its observation well. That lag
time is depended on character of aquifer and observation distance.
. The spread velocity of water head is
function of catchment rate, and water and solid media is more compressive , the
spread velocity is more little. In fact ,there is a lag time between the water
level change of well in confined aquifer and its observation well. That lag
time is depended on character of aquifer and observation distance.
Keywords: Confined aquifer; Stagnant flow; water head spread; Wave equation
Meizer is the first to realize the compressibility of confined aquifer[1]. Traditionally, the unstable water level change of well in confined aquifer was based on the instantaneous spread of water head. But , generally, in the pumping test we can observe that the change of the water level in the pumping well does not instantly lead to that of the observation well, that is to say, there is a time span or lag time for the process of the spread of water level in seepage field. That lag time has something to do with the character of aquifer, the character of water and the distance of water heads. Based on the infiltrative damping theory[2][3], porous wall can be regarded as the obstacle to linear movement of sticky liquid. In fact, just because of the block effect of media[4-6], the spread of water head gets a certain velocity. Muskat believes that the velocity of confined aquifer is similar to that of sound[7]. Meinzer agrees with Muskat on that point and believes that quantitative criterion of the velocity is related to the level of measurement. Owing to the condensability of solid media and water media, there lies a process of attenuation and adjustment to water pressure in media, which can be called lag time. In this paper, inertial equation is derived by applying contiguous media dynamics theory; parameter of the spread of water head is obtained and meanwhile its physical significance is stated.
1 The Inertial Transport Equation
We base our seepage flow research on representative elementary volume(REV), suppose single composition water and porous solid media as continuous media which permeate the whole space. From this point of view, we generally believe that the relationship between seepage velocity and specific capacity is like this[2][3][8]:
![]() (1)
(1)
in this equation, ![]() ——specific capacity,dimension
LT-1;n
——porosity,without dimension;
——specific capacity,dimension
LT-1;n
——porosity,without dimension;![]() ——seepage velocity,dimension : LT-1. formula (1)is
sometimes called Dupuit-Fochheimer equation.
——seepage velocity,dimension : LT-1. formula (1)is
sometimes called Dupuit-Fochheimer equation.
Suppose f(x,t) as a certain physical quantity, such as mass, density, momentum and energy .
![]() is the
system density, n is the system hole
distribution ratio, U(t)is the volume of system at the time of t (fig.1), then from Renold transport
equation, we can get the equation,
is the
system density, n is the system hole
distribution ratio, U(t)is the volume of system at the time of t (fig.1), then from Renold transport
equation, we can get the equation,
![]() (2)
(2)
in this eqution, ![]() is the volume of controlling body;
is the volume of controlling body;
![]() is seepage;
is seepage; ![]() is system volume;and
is system volume;and ![]() represents the direction of the
normal line outside of control volume.
represents the direction of the
normal line outside of control volume.

Fig.1 The system and control volume of a aquifer
For
![]() (3)
(3)
and since ![]() , taking differential coefficient
calculation, and together with (1), (2) we can get
, taking differential coefficient
calculation, and together with (1), (2) we can get
![]() (4)
(4)
and (4) is the continuous equation of ground water seepage.
In order to get the transport equation, take a random entity whose mass is m, change its volume but keep its mass , then we get the momentum of this entity,
![]() (5)
(5)
taking differential coefficient calculation on (5), and together with (2) , we can get
![]() (6)
(6)
by Gauss law, taking (4) and (1) into consideration, we can get,
![]() ▽
▽![]() (7)
(7)
![]() agrees with the composition of forces on
agrees with the composition of forces on ![]() , including
surface force
, including
surface force![]() ,entity
force
,entity
force![]() , and infiltration resistance
, and infiltration resistance![]() .
.
The expression of surface force is,
![]()
here, ![]() ,which is a tensor,
,which is a tensor, ![]() is the direction of outside normal line.
is the direction of outside normal line.
Using gauss law on this equation, we get,
![]()
In the
traditional hydrodynamics only surface force and entity force are taken into
consideration. ![]() is related to the fluidity of
liquid and changes with pressure , temperature and so on. If water is static in
porous media, the value of
is related to the fluidity of
liquid and changes with pressure , temperature and so on. If water is static in
porous media, the value of ![]() is 0. Another example, when
is 0. Another example, when ![]() ,
,![]() .
.
Thus, we can get a movement equation:
![]() ▽
▽![]() (8)
(8)
In Cartesian Coordinates, make the up direction
of z positive, suppose ![]() is acceleration of gravity, then
the inner entity force of
is acceleration of gravity, then
the inner entity force of ![]() is
is ![]() , unit entity force is
, unit entity force is ![]() . Surface force is the pressure
from nearby representative elementary volume, so
force can only act on the controlling body
. Surface force is the pressure
from nearby representative elementary volume, so
force can only act on the controlling body ![]() , surface force
, surface force ![]() ▽
▽![]() .
.
Finally, suppose infiltration resistance ![]() and
and ![]() in ground water seeping field takes on linear
relationship(agrees with linear law). Its proportion coefficient is
in ground water seeping field takes on linear
relationship(agrees with linear law). Its proportion coefficient is ![]() ;
;![]() is dynamic viscous coefficient, dimension : ML-1T-1;
is dynamic viscous coefficient, dimension : ML-1T-1;![]() is infiltration rate, dimension L2; thus the infiltration
resistance for volume unit is:
is infiltration rate, dimension L2; thus the infiltration
resistance for volume unit is:
![]() (9)
(9)
then, (8) can be turned into(10)
![]() ▽
▽![]() ▽
▽![]() (10)
(10)
in Darcy law, suppose the area of application is
laminar flow state and the item of inertia is not considered, ![]() and
and ![]() are both constant. For
are both constant. For ![]() ,
, ![]() , thus
, thus ![]() 。(10)is turned into
。(10)is turned into
![]() ▽
▽![]() (11)
(11)
And (11) is namely 达西 equation[9]. It is an approximate law in certain special condition.
In (9), the first item local acceleration is much larger than the second item transport acceleration. In common cases, the transport acceleration can be ignored; thus we get the linear transport equation which includes the item local acceleration:
![]() ▽
▽![]() (12)
(12)
using water head, it can be expressed like this,
![]() ▽
▽![]() (13)
(13)
in this equation, ![]() ;
;![]() is infiltration rate,dimension L;
is infiltration rate,dimension L;![]() is dynamic viscous coefficient, its dimension is ML-1T-1.
is dynamic viscous coefficient, its dimension is ML-1T-1.
2 The Spread of Water Head in Confined Aquifer
The traditional Darcy equation is a linear diffuse equation. Water head spreads at unlimited velocity, i.e. the changes of water level can be spread everywhere in the infiltration field. Actually, there is a lag time between the water level changes of well in confined aquifer and that of its observation well and that lag time is depended on character of aquifer and the observation distance.
a) Physical significance of underground water movement equation
The
underground water movement equation, which
includes the acceleration item, is a damped equation which includes the time
unit ![]() . In common cases, water density
and viscous coefficient are the function of time and pressure, but their
changes are little under normal pressure and temperature. Here we suppose,
. In common cases, water density
and viscous coefficient are the function of time and pressure, but their
changes are little under normal pressure and temperature. Here we suppose,
![]() (14)
(14)
![]() , the first item in equation (13), shows the runoff
changes resulted from the unsteadiness of flow field. It is similar to the lag
time equation of heat exchange in isotropy media, which is discovered by
Cattaneo and Vernotte in their thermodynamics analysis research[9][10].
The dimension of
, the first item in equation (13), shows the runoff
changes resulted from the unsteadiness of flow field. It is similar to the lag
time equation of heat exchange in isotropy media, which is discovered by
Cattaneo and Vernotte in their thermodynamics analysis research[9][10].
The dimension of![]() is T, it has a time unit which stands for the lag time.
is T, it has a time unit which stands for the lag time.
b) Continuous equation expressed by water head
![]() and
and ![]() are function of compression
coefficient
are function of compression
coefficient ![]() in porous media(dimension N
in porous media(dimension N![]() L2)and compression coefficient
L2)and compression coefficient ![]() (dimension N
(dimension N![]() L2)in solid media. Their changes can be shown like
this,
L2)in solid media. Their changes can be shown like
this,
![]() (15a)
(15a)
in this equation, ![]() is the pressure of static water,
and its dimension is N
is the pressure of static water,
and its dimension is N![]() L2.
L2.
![]() (15b)
(15b)
Taking (15) into (14) with substitution method, in
view of ![]() ▽
▽![]() , and therefore we get,
, and therefore we get,
▽![]() (16)
(16)
When matter and temperature are kept unchanged in
compressive flow field, ![]() , and its underground water head
is,
, and its underground water head
is,
![]() (17)
(17)
Drawn from (16) and (17), we get (18)
![]() (18)
(18)
here, ![]() , is the catchment rate in
aquifer, its dimension L-1.
, is the catchment rate in
aquifer, its dimension L-1.
Take (13) into (17) with substitution method, and omit the quadratic differential coefficient of H, and we can get the continuous equation expressed with water head,
△![]() (19)
(19)
△![]() ,is Laplacian operator.
,is Laplacian operator.
3 Lag effect of Underground Water Head
Equation (19) is continuous equation of underground water seepage with inertia in it, and it’s a damped wave equation[11][12], different from traditional heat exchange equation. According to the physical significance of wave equation, the wave velocity or the spread velocity of water head in seeping field can be drawn,
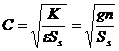 (20)
(20)
water head spread velocity is mainly the function
of ![]() . The greater the compressibility
of water and solid media is, the lower the spread velocity of water head is.
Generally speaking, in confined aquifer from fine sand to gravel, water head
spread velocity C is 41-185m/s, which is lower than
the velocity of sound.; correspondingly, water head spread lag time
. The greater the compressibility
of water and solid media is, the lower the spread velocity of water head is.
Generally speaking, in confined aquifer from fine sand to gravel, water head
spread velocity C is 41-185m/s, which is lower than
the velocity of sound.; correspondingly, water head spread lag time ![]() is quite little, less than one second.
is quite little, less than one second.
4 Conclusion
The character
of water head spread in confined aquifer is related to the solid media and
water media in aquifer, and its spread velocity is 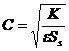 . Generally speaking, the thicker
the granule is, the higher the spread velocity of water head is, vice versa.
The well flow movement equation, taking water head spread into consideration,
which is different from Theis model, should contain the item of water head
spread parameter. When the lag time
. Generally speaking, the thicker
the granule is, the higher the spread velocity of water head is, vice versa.
The well flow movement equation, taking water head spread into consideration,
which is different from Theis model, should contain the item of water head
spread parameter. When the lag time ![]() is quite short, it can be turned into
the traditional confined aquifer Theis model. Therefore,
in lower penetrability aquifer containing mainly fine sand, the spread velocity
of water head is lower, and the lag time is longer. Taking water head lag
effect into account, the well flow equation is much similar to the conditions
of the real well flow.
is quite short, it can be turned into
the traditional confined aquifer Theis model. Therefore,
in lower penetrability aquifer containing mainly fine sand, the spread velocity
of water head is lower, and the lag time is longer. Taking water head lag
effect into account, the well flow equation is much similar to the conditions
of the real well flow.
In a serious hydro-activities such as water resource development and management, it’s quite important to know the distribution of hydraulic pressure field in underground water movement and its spatial changes. Taking water head spread lag effect into consideration in hydro-geology model will no doubt make the model more perfect to be more similar to the conditions of the distribution of real pressure in seepage field and reduce the calculation error at the beginning of the pumping test, and what’s more important is that during a certain period of time, it can simplify the border conditions, that is to say, the area outside of the water head spread border has no effect on each physical quantity(such as pressure, density, runoff and so on). In this way, we can greatly reduce the work of calculation and improve the precision of calculation.
Reference
[1] Zhang Hongren. Development of non stable flow in groundwater[M] .Beijing: Geology Press,1975: 1-32
[2] J.Bear. Fluids dynamics in porous media[M]. China architecture and building press,1983:12-246
[3] Scheidgger A.E. The physics of flow through porous media[M].University of Toronto Press, 1957:3-106
[4] Li Peicheng. Discussion on elastic drain theory and its limitation in confined aquifer[J]. Ground water,1984(2):8-11
[5]Chapuis R.P.,Chenaf D. Slug tests in a confined aquifer: experimental results in a large soil tank and numerical modeling[J]. Canadian Geotechnical Journal, 2002, 39(1):14-21
[6]Bachu, S.. Synthesis and model of formation water flow in the Alberta Basin , Canada[J]. AAPG Bulletin, 1995, 79:1159-1178.
[7] Muskat M. The flow of homogeneous fluids through porous media[M]. McGraw-Hill, 1973:45-123
[8] Guo Dongping. Basic theory of seepage flow. Shaan xi science and technology press,1994:56-283
[9] Fasaro A., Primicerio M. General free boundary problem for the heat equation [J]. J. Math. And Appl. 1977,59(1):1-14
[10] Angulo J.M., Ruiz-Medina M.D., Anh V.V., Grecksch W., Fractional diffusion and fractional heat equation[J]. Adv. Appl. Prob. 32 (2000) 1077-1099.
[11] Mohamed F.A., A damped wave equation for groundwater flow, advanced in water resource[J].1990 (15):117-223
[12] Lu Yudong, Li Peicheng.The Study of Time-dependent Boundary Model of Inconstant Well Flow in Unconfined Aquifer Ground Water Flow Due to Hydrodynamic Lag[J]. Journal of irrigation drainage, 2005,24(2):27-30.




