Achievements
APPLICATION OF THE MANAGEMENT MODEL ON CHANGMA IRRIGATION AREA OF THE SHULE RIVER
Jin Shenghai , Yin Miying
Institute of hydrogeology and Environmental Geology, CAGS,
Abstract: The paper aims at setting up the multi-management model in consideration of the concrete situation in the studied area for the optimization of water resources used for Changma irrigation area based on the result of the model.
Key words: The Shule River area, Multi-management mode, Optimal scheme
1 Basic Situation in the Studied Area
The
2 Setting up the Management Model
2.1 Clew
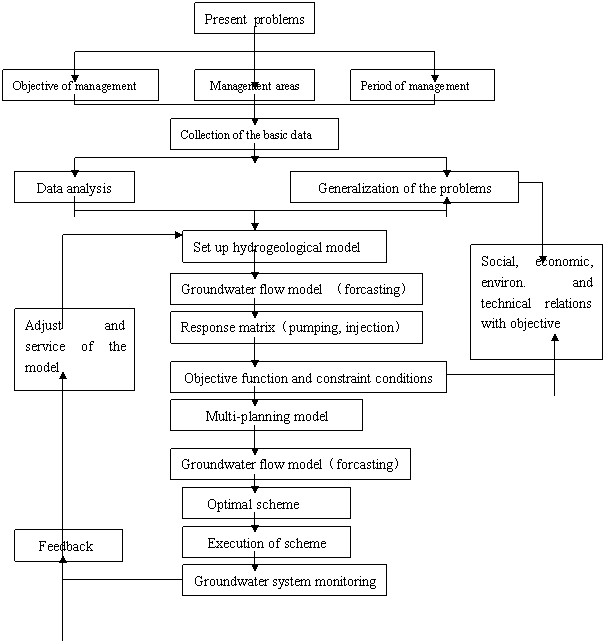
Over years of the practice, the water resources management model is an available way to solve the issue in this area where the water resource system is a synthesis of multi-factors. The change from any of the factors can impact the whole system and even effect the local ecological environment. The optimal allocation of the water resources can meet the requirements of Industry, agriculture and domestic purpose,meanwhile,control the occurrence of secondary salinization and dertification (Fig.1).
2.2 Setting up the management model
The studied area is systematically generalized to determine the management scheme. It is also divided into subzones for the purpose of management including the goal constraint and resource control that separate from the real situation.
The studied area can be divided into 10 subzones according to the distribution of the irrigation area, ecologyical environment, administrative zones and developing planning and 71 response spots are set there (Fig.2)
The basic model is as follows:
 Allowable exploitation amount in the management area;
Allowable exploitation amount in the management area;
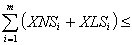 Potential surface water amount in the management area;
Potential surface water amount in the management area;
 total water amount of Agriculture, livestock and people, forestry needed in the i area (i=1,2,…,m);
total water amount of Agriculture, livestock and people, forestry needed in the i area (i=1,2,…,m);
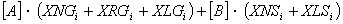 >or<allowable dropdown of water level (i=1,2,…m);
>or<allowable dropdown of water level (i=1,2,…m);
Where>or<allowable dropdown can be determined according to the practical situation.
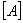 —— Response matrix by pumping water
—— Response matrix by pumping water
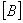 ——Response matrix by injection of surface water
——Response matrix by injection of surface water
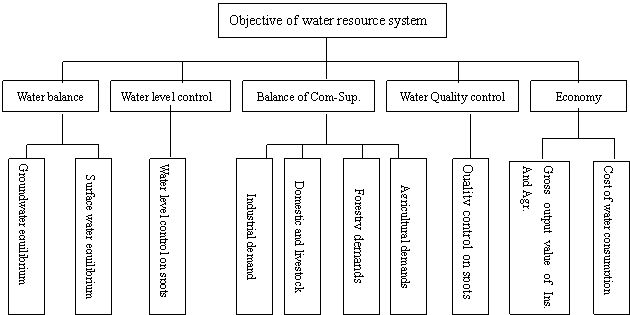
Fig.1 Ideal water resource system planning

Fig.2 Distribution of the subones
3 Setting up Mathematical Model
3.1 Mathematical model
Based on the basic model,a multidimensional objective function can be set to meet the requirements of constraint conditions and come at a set of decision variable solution to keep the minimum deviation between the decision and the given object. The following is the mathematical model:
Objective function 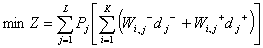
Goal constraint 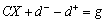
Resource control 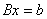
Variable constraint 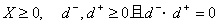
 is the number of objective constraint;
is the number of objective constraint;
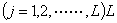 is the level of objectives;
is the level of objectives;
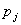 ——Priority level
——Priority level 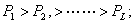
![]()
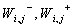
 Weighting factor;
Weighting factor;
![]()
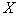
 Decision variable;
Decision variable;
![]()
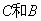
 Coefficient matrix corresponding to constraint conditions;
Coefficient matrix corresponding to constraint conditions;
 Negative deviation;
Negative deviation;
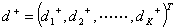 Positive deviation;
Positive deviation;
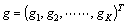 Goal value;
Goal value;
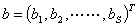 Resource control value,S is the number.
Resource control value,S is the number.
Objective planning can be with a common measure to balance the objectives at different grades, but at the same grade the dimension of the objective must be equal. The objectives at different grades can even be contradictive between one another. The decision makers must decide the order according to their importance. Afterwards, they can work accordingly. The order must first meet the higher objective’ requirement and then go on in turn downwards. The lower objective has to submit to the higher objective when they are contradictive. The surface water is taken as the most important water source so that it is the first objective in this study. The rest may obtain different weighting factors according to their importance as well in this study.
3.2 Objective function
The six objectives are drown up according to the basic model in the studied area:
The first objective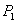 :Surface water used is less than the potential surface water supply;
:Surface water used is less than the potential surface water supply;
The second objective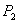 :Groundwater exploitation is less than the allowable exploitation of groundwater;
:Groundwater exploitation is less than the allowable exploitation of groundwater;
The third objective :To meet the requirements of people and livestock water supply;
:To meet the requirements of people and livestock water supply;
The fourth objective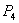 :To meet the agricultural purpose;
:To meet the agricultural purpose;
The fifth objective :To meet the forestry requirement;
:To meet the forestry requirement;
The sixth objective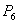 :Dropdown of groundwater level has to avoid the effect on ecological environment.
:Dropdown of groundwater level has to avoid the effect on ecological environment.
The expressions are:
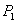 :
: 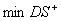
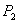 :
: 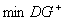
 :
: 
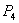 :
: 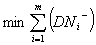
 :
: 
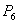 :
: 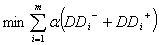
where:
![]()
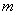
 The number of the subzones;
The number of the subzones;
![]()

 The number of the responses;
The number of the responses;
![]()
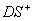
 The positive deviation of water supply from the surface water in the management area;
The positive deviation of water supply from the surface water in the management area;
![]()
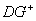
 The positive deviation of the allowable exploitation in the management area;
The positive deviation of the allowable exploitation in the management area;
![]()
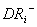
 The negative deviation of water used by people and livestock in the i subzone;
The negative deviation of water used by people and livestock in the i subzone;
![]()

 The negative deviation of agricultural needs in the i subzaone;
The negative deviation of agricultural needs in the i subzaone;
![]()
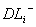
 The negative deviation of the forestry demand in the i subzone;
The negative deviation of the forestry demand in the i subzone;
![]()
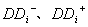
 The negative or positive deviation of groundwater level dropdown at the i response dots;
The negative or positive deviation of groundwater level dropdown at the i response dots;
![]()
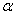
 The weighting factor of dropdown.
The weighting factor of dropdown.
Objective function is:
Where: + = to meet the requirements in turn rather than the relations of algebraic sum
m=10, n=71
3.3 Constraint conditions
The constraint conditions are mainly from the surface water used constraint, groundwater exploitation constraint, water supply objective constraint, water level drawdown constraint, spring water constraint, non-negative constraint (All the decision variables and positive-negative deviations cannot be equal to zero.)
4 Results and Anlyses
4.1 Model solving
The solution of the model takes from “Groundwater Management Model” written by Lin Xueyu but revised here and there. The way to solve the objectives is based on the ordering goal programming,that is the multi-objectives can be divided into the single objective model according to the priority. The results include the optimal variable, the minimum deviation and the optimal objective value(Table 1).
Table 1 Results of the model solved in the Changma Irrigation area
Subzones Water amount(mil.m3/a) | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Total | Deviation |
Surface water | 64.40 | 99.64 | 68.26 | 96.46 | 12.19 | 39.75 | 43.18 | 423.88 | 0 |
Groundwater | 50.00 | 0 | 5.60 | 0 | 32.30 | 0 | 40 | 127.90 | 0 |
Total | 114.40 | 99.64 | 73.86 | 96.46 | 44.49 | 39.75 | 83.18 | 551.78 | 0 |
4.2 Result analysis
From the table above, the result is clear that the objectives are restrict with each other. The water quantities meet the demands that some unreasonable allocation still remains in some of the subzones. For example, the Ⅶ subzone needs surface water for irrigation, for this area needs reclaimation of saline soil, therefore, there is no need of groundwater except pumping out some groundwater for the domestic use or livestock. Yet groundwater is zero in the Ⅱ,Ⅳ and Ⅵ subzones. There is no way to meet the requirements of water supply. As the result, the man intervention can help solve such problems by adjusting the quantities of
water supply. The final result must be balanced.
4.3 Optimal scheme
The surface water quanlity is 42.17 mil.m3/a in the Changma irrigation area. The groundwater exploitation is 89 mil. m3/a, therefore, groundwater exploitation increases about 25.31mil. m3/a,but decrease surface water demands (Table 2).
In general, the optimal scheme is rational as the practical situation is considered. However, no objective is perfect so that we make another way to examine the scheme if it can meet the requirements by comparing them.
Table 2 The scheme corrected in the Changma irrigation area
Subzone Water amount (mi. m3/a) | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Total |
Surface water | 9134 | 6957 | 6750 | 9646 | 1495 | 3975 | 4213 | 42170 |
Groundwater | 2000 | 3000 | 560 | 120 | 2951 | 159 | 110(3890) | 8900 |
Remark | 38.90 million m3/a groundwater should discharge off the area in the VII subzones and the irrigation water is just from the surface water. | |||||||
Table 3 Balance of groundwater in the Changma irrigation area in 2035
Amount of balance(mil. m3/a) Area | Changma | |
Recharge | Infiltration from the river | 418.69 |
Seepage from ditches | 130.31 | |
Field seepage | 136.54 | |
Flooding infiltration | 28.65 | |
Lateral inflow | 2.69 | |
Total | 716.87 | |
Discharge | Transpiration | 34999.35 |
Spring ovrflow | 10018.93 | |
Lateral flow | 167.79 | |
Pumping | 12810.00 | |
Total | 57996.07 | |
Difference between recharge and discharge | +13691.39 | |
The calculation shows that the groundwater level will be 3
So, the optimal management scheme is as follows: