Xiao Changlai¹, Liang Xiujuan¹, Feng Bo¹; Liang Xufeng²; Cui Jianming³，Zhang Jun³，Li Shulan³

1. College of Environment and Resources, Jilin University, Changchun, 130026, China;

2. College of Environment Engineering, Changan University, Xi’an, 710064, China;

3. Water Resources Management Office of Qian’guo County, Songyuan City, Jilin, 121200, China)

Abstract: Abundant ground water resources is buried and distributed in the valley of Songhua River. The determination of aquifer’s parameters is an important basis for groundwater resources evaluation, numerical simulation, development and protection as well as scientific management. Pumping test is a main method for determining aquifer’s parameters. A New method, called whole curve matching method (WCMM), is presented for determining confined aquifer’s parameters by using optimum theory together with computer technology on the basis of Theis equation for the pumping test in confined aquifers. A case study shows that this method has rapid speed and high accuracy. The results of parameter’s determination are optimized so that it has important practical value for scientific research and engineering practice.

Key words: Songhujiang river plain; aquifer’s parameter; pumping test; Theis equation; Whole Curve Matching Method (WCMM); confined aquifer

1 Introduction

The aquifer’s parameters include hydraulic conductivity (K), transmissivity (T), specific yield (m), storage coefficient (m*), leakage coefficient (b) , radius of influence (R)

(CHEN Yusun, YAN Mingzhi, 1985; CHEN Chongxi, 1985. XUE Yuqyun, ZHU Xueyu, et al. 1997) and so on. The determination of aquifer’s parameters is an important basis for groundwater resources evaluation, numerical simulation, development and protection as well as scientific management. Generally the methods to determine aquifer’s parameters includes pumping test method (YANG Tianxing, FU Zezhou, etc., 1980. GU Weici. 2000), water pressure method, water inflow test method, tracer method, indoor experiment method, regime data analysis method, numerical method, isotope method, numerical inversion method (FANG Peixian, et al, 1996), hydrochemistry dynamics method (CAO Yuqing, HU Kuanrong. 1994) and so on. Among these, pumping test is the main method to determine the aquifer’s parameters.

Pumping test can be classified according to the types of the aquifers (unconfined and confined aquifers), the flow conditions (steady and unsteady flows), the well characteristics (fully penetrating and partly penetrating wells) and the numbers of the wells (single well, group wells, interference well). For different pumping tests, different methods are required to determine the parameters. In the traditional pumping test, steady flow method or unsteady flow method can be used to determine the aquifer’s parameters. The Dupuit equation is adopted for the steady flow of the phreatic and confined water. Theis curve method, Jacob straight-line method, inflection-point method and water-level recovery method(SUN Gengsheng, et al., 2000; LI Tongbin, ZOU Lizhi, et al, 1995; Jacob Bear ,1979;    Ralph C. Heath, 1987; ZOU Lizhi, et al,1994) can be adopted for the confined unsteady flow. The modified Theis equation, Boulton modal, Neuman model and water-level recovery method can be adopted for the phreatic unsteady flow.

In recent years, the computer technology has been widely used to determine the aquifer’s parameters. The computer curve-matching method can overcome the inaccuracy caused by the subjectivity completely, and improve the efficiency greatly. The computer software has rapid computing speed, and it also can choose or delete abnormal data points on the screen, as well as to recalculate (ZOU Lizhi, et al,1994; ONG Xiaomei, CHEN Zhaoyan, 1996; HAO Qisheng, 1996; ZOU Zhengsheng, Zheng Jieqing, 2001). A great number of computer softwares have been presented in other countries to derive the aquifer’s parameters, such as Aquifer Test, AQTESOLV, Aquifer Test Pro 3.5, Aquifer Win32, PEST. The methods mentioned above do not take the data of the pumping process and recovery process into account at the same time when the parameters are determined.

In fact, no matter what methods are adopted, the aquifer’s parameters should be unique. In this article, we adopt traditional methods and present whole curve-matching method, together with the pumping test data from a certain water source field, to determine the confined aquifer’s parameters, and has got satisfactory conclusions.

2 General Situation of the Study Area

The alluvial plain of the Songhua river is located along the both banks of the Songhua river. It is 4~7 km wide, very flat and composed of flood plain and the first river terrace. The pore aquifer with coarse grains and big thickness is generally buried in the plain. The ground water is abundant in the plain and become the important water sources for the cities and towns along the river.

The study area lies on the valley alluvial plain of the Songhua River, Jilin Province , Northeast China. Quaternary is well-developed. The Holocene (Q₄) alluvial layer is 21.00~ 23.00m thick, which has two-layer construction. The upper layer consists of silty clay 2.50~4.00 m thick; the lower layer consists of sand and gravel (coarse sand and gravel, pebbles) 16.00~18.00 m thick, and the latter form a good unconfined aquifer. Middium Pleistocene (Q₂) is a set of lacustrine deposit, which mainly consists of muddy loam 24.00~28.50 m thick. Its permeability is low and it forms a relative aquiclude which is the lower confining bed of the unconfined aquifer and the upper confining bed of the confined aquifer. The Lower Pleistocene (Q₁) Baitushang Formation (Q_1b) is a set of glaciofluvial deposit, which mainly consists of sand and gravel (coarse sand and gravel, pebbles) with loam or clay beds. In this formation the particles become coarser from the upper part to the lower part, and there is often gravel at the bottom. This layer is 1.00~4.00 m thick and form a good confined aquifer. The depth of the upper confining bed is 47~49.50m. The underlying bed is Upper Cretaceous (K₁), which is lacustrine deposit layer consisting of black or gray mudstone with a great thickness. Only the surface of the mudstone has a crust of weathering about 0.50m thick and the lower mudstone is dense and hard. It forms the regional lower confining bed due to the low permeability.

3 Main Principle for Parameter Computation

3.1 Theis equation

When the lateral boundaries of the confined aquifer are quite far away from the wells and the boundaries have little effect on the distribution of the water heads in the research areas, the aquifer can be considered as an unbounded aquifer without recharge. When the pumping rate is constant, the corresponding mathematical equation for confined groundwater flow to fully penetrating well is called famous Theis equation, which is:

(1)

(2)

Where s=Ho-H, which is a certain point’s drawdown at any time in the area influenced by the pumping (m); Ho is the initial water head; H is the water head after pumping; Q is the pumping rate (m³/d, m³/min); W (u)is the well function, which can be inquired by corresponding forms; T=KM, which is the transmissivity of the confined aquifer (m²/d, m²/min); K is the hydraulic conductivity (m/d, m/min); M is the thickness of the aquifer (m); a is the pressure-transmission coefficient of the confined aquifer (m²/d, m²/min); t is the period from the beginning of the pumping to the calculation time (d, min); r is the distance from the observation well to the pumping well (m); m* is the storage coefficient of the confined aquifer.

For convenience, generally W (u) is expanded into series:

(3)

During the recovery period, the residual drawdown is:

(4)

 (5)

(6)

Where s’ is the residual drawdown (m); t_p is the period during which the pumping rate is held constant (d, min); The other parameters’ meanings have been mentioned before.

The traditional methods using Theis equation to determine the aquifer’s parameters mainly include Curve-matching method, Jacob straight-line analysis method and water-level recovery method. The best advantages of Curve-matching method are that it can completely adopt all the data of the pumping test, and avoid the accidental inaccuracy caused by certain individual data and improve the accuracy. The disadvantages include that, first, in the early stage, the actual curve doesn’t match well with the type curve, so the period of unsteady pumping test shouldn’t be too short; second, in the latter stage, when the curve is fairly flat, it is difficult to match with the type curve correctly, thus inaccuracy may come out due to the individual judgment. So when we determine the continuous period of pumping and the accuracy of the observation, we should take the bending part of the s-t or s-t/r² curves which can be drawn according to the data into account to match the type curve; if the data in the final stage deviates the type curve, it may be caused by the influence of the boundaries outside the aquifer or by changes in the rock characteristic of the aquifer. The advantages of Jacob straight-line analysis method are that: it can avoid the randomness in Curve-matching method, and it can completely use all of the data in the latter pumping period; however, it must satisfy the requirement of u≤0.01 or u≤0.05, that is to say, only in the conditions that r is rather small while the t is fairly long can this method be adopted; otherwise, if the pumping period is too short, both of the slope of the straight-line and the intercept are small, all of which may lead to a greater transmissivity (T) as well as a smaller storage coefficient (m*).

3.2 Whole curve-Matching method

No matter curve-matching method, straight-line analysis method or water-level recovery method mentioned above, the parameters derived are the data from parts of the pumping process, or all of the data from the pumping process (as to curve-matching method) as well as parts of the data (as to straight-line analysis method), or only the data of the water-level recovery (as to water-level recovery method), without taking the data of the pumping process into account together with the data of the water-recovery process. That is why in the same aquifer, different methods lead to different parameters. Sometimes the great differences between the parameters that are determined by different methods may bring lots of troubles in the evaluation and development of the groundwater resources.

While in this article, a new method is put forward, which not only takes the whole process of the confined aquifer pumping test into account but also takes advantage of all the data of the pumping process, including the data during the pumping process and recovery process. It is a method to adopt whole curve-matching method together with Theis equation and optimizing theory to determine the aquifer’s parameters.

(1) During the pumping period

Target function is：

Z = min∑( s_m- s_c)²       (7)

Constraint condition, under which theoretical curve matches best with the actual curve of the pumping test, is:

Absolute error: s_m-s_c ≤ e₁

Relative error: (s_m-s_c )/ s_m ≤e₂             (9)

where s_m is the actual drawdown (m); s_c is the calculated drawdown (m), which can be determined by equation (1)~ (3) after T and m* are defined; e₁ is the allowable absolute error of the drawdown (m); e₂  is the allowable relative error of the drawdown (%).

(2) During the water-level recovery period

Target function is：

Z = min∑(s_m-s_c)²  (10)

Constraint conditions, under which the pumping test theoretical curve matches best with the actual curve ,  is:

Absolute error: s׳_m-s׳_c ≤ e₁   (11)

Relative error: (s׳_m-s׳_c )/ s_m ≤e (12)

where s׳_m is the actual residual drawdown (m); s׳_c is the calculated residual drawdown (m), which can be determined by equation (4)~ (6)after T and m* are defined; e₁ is the allowable absolute error of the drawdown (m);   is the allowable relative error of the drawdown (%).

The calculation process can be done by programmed computer or by software Excel. Adjust the parameters T and m* continuously, while keeping the values uniform during the pumping period and the water-level recovery period. If these conditions are fulfilled, in other words, the sum of squares of the errors between the actual measured value and the calculation value of the drawdown is minimum, the parameters (T and m*) of this time are what to be solved. In this way can the aquifer’s parameters be ensured unique, reliable and optimal. If there exist individual abnormal points, they can be deleted by analyzing the causes to ensure the aquifer’s parameters to be reliable and excellent.

The Whole curve-matching method mentioned in this article can be directly used to determine the unconfined aquifer’s parameters when the drawdown is very small and when the drawdown is modified as s׳= s-s²/2H if the drawdown is big, where H is the initial thickness of unconfined aquifer and s is measured drawdown.

4 Results and Discution

There are 9 hydrogeological boreholes with the total depth of 409m, among which there are 2 confined pumping wells (CH₁, CH₂) and 2 observation wells (G₁, G_2q). After many times’ pumping tests, a great number of data have been got. Then the hydrogeologic parameters of the aquifer which is to be developed can be determined with the corresponding methods (Theis Curve-matching method, Straight-line analysis method and Water-level recovery method) of the pumping tests in confined aquifer. Meanwhile whole curve-matching method mentioned in this article is adopted to determine the corresponding hydrogeological parameters. (See Table 1)

Table 1 Results of the confined aquifer’s parameters

Table 1 shows that the aquifer’s parameters determined by traditional methods may have a little difference resulting from the different methods, while the difference may sometimes be great for a certain individual parameters. So it is difficult to select the best ones among the results. If the parameters are selected without giving a comprehensive and careful consideration of the hydrogelogical conditions, the chosen parameters may possibly deviate from the matter of fact. The parameters determined by Whole curve-matching method mentioned in this article are almost equal to those determined by the traditional

methods, because this method makes full use of all the information during the pumping tests, including all the data during the pumping period and the water-level recovery period, and properly neglects some individual abnormal points to ensure the conditions under which the sum of squares of the errors between the measured drawdown and calculated drawdown is minimum, the type curve matches well with the actual curve, therefore it avoids the influence of human, and ensure the aquifer’s parameters deprived to be unique , reliable and excellent (Fig.1 and Table 2).

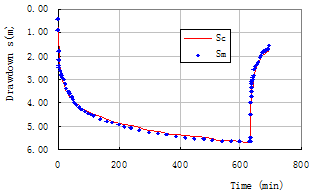
Fig.1 Drawdown matching curve for Observation well G1 when well Ch1 is pumping

Table 2 Compared table of Calculated and measured drawdown

5 Conclusion

The advantages of Whole curve-matching method include that it can be used to determine the parameters quickly and correctly, and avoid the influences of human; it makes full use of all the information during the pumping tests, including all data during the pumping period and during the water-level recovery period, properly neglects some individual abnormal

points and ensures the conditions under which the sum of squares of the errors between the measured actual drawdown and calculated drawdown is minimum, the type curve matches well with the actual curve, while ensure the aquifer’s parameters deprived to be unique , reliable and excellent.

This method can also be used to determine unconfined aquifer’s parameters. So it has great value in practice and application.