QI Deng-hong

(Geological Environment Monitoring Institute of Henan, Zhengzhou Henan, 450006, China)

 

Abstract: Accurately calculating the quantity of rainfall infiltration recharge (RIR) to groundwater is critical importance to the evaluation and management of groundwater resources. Enormous works have been done to estimate the quantity of RIR and to understand the processes of infiltration recharge by many methods including field tests, lysimeters and etc. There are 35 lysimeters with 7 kind of soil and 5 different depth (1m, 2m,3m, 5m and 7m) installed in Zhengzhou Groundwater Balance Test Field to measure the infiltration recharge flux and evaporation flux under conditions of fixed water tables at the bottoms of the soil columns. A simple meteorological observation has built to measure the rainfall, wind rate and water evaporation on ground surface. Some key infect factors have been chosen to construct the rainfall infiltration recharge functions (RIRF) for different kinds of soil after the relationship between the RIR and rainfall and evaporation in the corresponding and former period by uniform design method. Comparing the measured data with the calculated data by RIRF, the small difference denotes that using the RIRF can calculate the RIR more accurately than conventional method of product of rainfall and constant RIR coefficient.

Key words: lysimeter; regression analysis; rainfall infiltration recharge function (RIRF); uniform design

 

1 Introduction

The process of rainfall goes into groundwater through soil is called rainfall infiltration process; the groundwater recharge is called rainfall infiltration recharge (RIR). It is the main driving force of surface contaminant polluting groundwater, and is also the main recharge source of groundwater. Accurately calculating the quantity of RIR to groundwater is critical importance to the evaluation and management of groundwater resources. In the past groundwater estimation, groundwater fluctuation data is often used to ascertain rainfall infiltration coefficient, which is multiplied by rainfall to calculate RIR. In 70^s and 80^s of 20^thcentury, many equilibrium experimental points were built in China, where can use lysimeter observing RIR, and calculating rainfall infiltration coefficient for evaluating the groundwater resource^[1,2]. 

Rainfall flux, rainfall characters, lithologic characters of unsaturated zone, groundwater depth, and human activities are the factors affect RIR, part of which exist nonlinear relationship. Moreover, hysteresis and delayed reaction occurred in rainfall infiltration^[3-8]. So RIR is a nonlinear function affected by many factors. But in the past groundwater resource estimation, RIR is considered as a linear function of rainfall (rainfall infiltration coefficient is a constant), which has a big error to the facts, so it affects the accuracy of groundwater resource evaluation.

Influencing factors of RIR are selected through analyzing the observed data of equilibrium experimental points in Zhengzhou and correlation analysis. Rainfall infiltration function is established by using regression analysis that studied the relationship between RIR and influencing factors, which can analysis the rule of RIR.

2 Influencing Factors Choosing

2.1Main influencing factors

After rainfall infiltration, calculating initial soil moisture distribution is a considerable factor, because it determined the velocity of rainfall infiltration and soil moisture storage in unsaturated zone, and can affect final infiltration recharge. According to the soil moisture equilibrium principle, rainfall, evaporation and infiltration recharge controlling mainly determine soil moisture in unsaturated zone, and initial soil moisture is mainly affected by rainfall, evaporation in a period of time before calculating. So regression model of RIR is as follows:

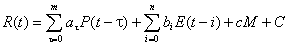             （1）

where,  M is groundwater depth[L]；a、b、c、C are constant; m、n are prophase rainfall, time length of water evaporation respectively, which can be evaluated different values because of different influencing degree between rainfall and evaporation. Using experiment-designing method can derive the reasonable value. Because RIR decreasing as groundwater depth increasing when depth exceed 1m,linear format is denoted for establishing unified model.

2.2 Establishing model method and process

Regression model consider evaporation and groundwater depth in different periods except different periods of rainfall. Especially evaporation needs consideration, because former evaporation will affect RIR. Usingtrial method derives the numbers of former rainfall and evaporation in order to get better result through less former rainfall and evaporation.

2.2.1 Uniform design abstract

The purpose of uniform design is to derive satisfied parameters using least experiments. Uniform design is a experiment designing method of many factors and many levels which invented by two Chinsesemathematicians named Fang Kaitai and Wang yuan, it is a scientific method of distributing testing spots uniformly in experimental range, which can get reasonable result especially for large range and many factors or levels of experiments^[9].   

Uniform design often uses a uniform table U_n（q^s）and corresponding tables, U represents uniform design; n represents numbers of experiments, q represents numbers of levels; s is numbers of columns which can arrange numbers of s factors. Every uniform design table is accompanied by a introduction table, which explains degree of homogeneity of experiment.

    The steps of uniform design is as follows, 1）choosing reasonable factor and level based on the purpose of experiment；2）listing the factors and their levels on the column and the row according to the index of the number chosen from the chosen reasonable uniform design table and use table.

2.2.2 Establishing model process

After the ranges of rainfall and evaporation and their experiment levels have been determined, the test scheme is determined using uniform design method. The average values of error square (AES) of every test are calculated. The minimum ASE is determined by Krige method. The new test schemes with miner interval near the column and row of minimum ASE are determined by uniform design. The AES of new test schemes is calculated and the process repeats until getting the most suitable number of former periods of rainfall and evaporation that are used to regression analysis.

3 Rainfall Infiltration Recharges Function

     The annual and monthly RIRFs of different soils are determined with this method.

3.1 Annual rainfall infiltration recharge model

Annual RIR has little relationship with rainfall and evaporation in the former period and evaporation in the corresponding period according to the former analysis. The RIRF can be descried by the follow equation.

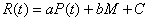          （2）

The coefficients of equation 2 derived from measured data about rainfall, RIR and evaporation by regress analysis method are listed in table 1. According to the regress results, RIR is positive correlation with rainfall, but is negative correlation with buried depth of groundwater level. The sensitivity of RIR to buried depth of groundwater level is largest in silt from Xinxiang, and second in fine sand from Kaifeng, and least in silt clay from Zhumadian shown that its recharge mainly derived from preferential flow.

Table 1 Regression coefficients of the annual RIR to rainfall and buried depth of groundwater level in different soil lysimeters.

 

3.2 Monthly rainfall infiltration recharge function

The numbers of former periods of rainfall and evaporation are both less than 10 according to the former analysis, so 10 tests listed in table 2 are made under the directed by uniform design. The corresponding determining coefficient, F value and ASE are calculated respectively. Comparing the three characteristic values, the best m and n are used to determine the regression function and their regression coefficients are listed in table 3. The coefficients of infiltration recharge functions show that the RIR is mainly affected by the rainfall of two months before and the same month rainfall counts for 58~ 67% of all rainfall. Monthly RIR is negative correlation to monthly evaporation, especially the last past monthly because it evaporated more water from soil in lysimeter, which may be led more water stay in soil instead of recharging groundwater. When the buried depth of groundwater level is more than 1m, the RIR decreases with the buried depth of groundwater level. The decreasing rate is largest in loess loam, and it is decreasing in loam, light loam, loan with silt interbed and fine sand. But the inverse phenomena occur in loam from Zhumadian, which may be led by the ruleless macro pores or cracks and strong preferential flow in the lysimeters.

Table 2 The test scheme for monthly RIRF

Table3 Coefficients of monthly RIRFs

 

Fig.1 shows that the difference between monthly recharge data measured with calculated by regression function, which shows the monthly RIRF constructed by regression analysis can be used to calculate the RIR.

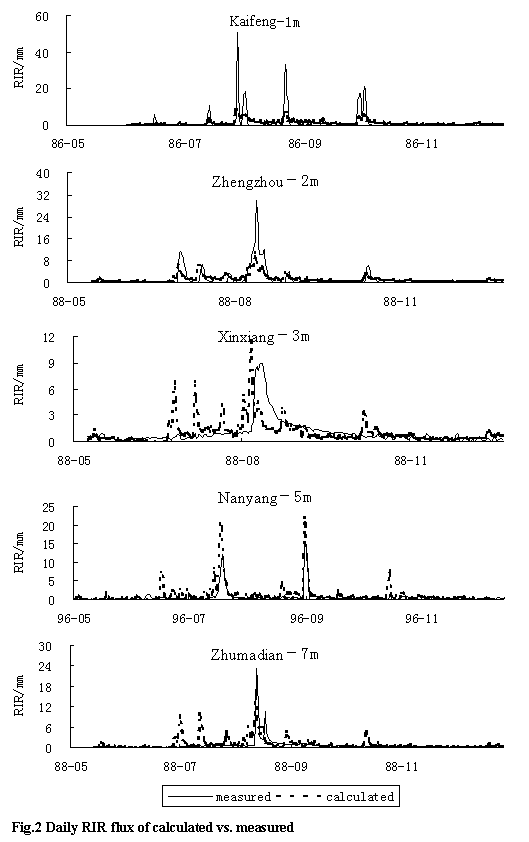
3.3 Daily rainfall infiltration recharge function

The values of m and n are less than 120 days i.e. 2 months according to the monthly RIRF. 24 tests with an interval of 5 days were taken under the direction of uniform design, and their determining coefficient, F value and ASE are calculated respectively. With the same method above, the best m and n are used to determine the regression function and their regression coefficients are listed in table 4. Fig.2 shows that the difference between the measured data and calculated data by daily RIRF is large, especially of shallow buried depth of groundwater table, which may be led by the non-linear correlation between RIR and buried depth of groundwater table, and the delay of infiltration recharge make the dairy RIR is little correlation to the daily rainfall.

4 Conclusions

The RIRFs with different time scale are established by regression analysis with rainfall and evaporation in same or/and former periods. Among the functions, annual and monthly infiltration recharge function is well to calculate the recharge. RIR is positive correlation with rainfall, but is negative correlation with buried depth of groundwater level. The sensitivity of RIR to buried depth of groundwater level is largest in silt fromXinxiang, and second in fine sand from Kaifeng, and least in loam from Zhumadian shown that its recharge mainly derived from preferential flow. For monthly scale, RIR is mainly affected by the rainfall of two months before and the rainfall in the same month counts for 58~67% of all rainfall. The daily RIRF is less accurate because of the delay of infiltration and the irregular temporal distribution of rainfall.

 

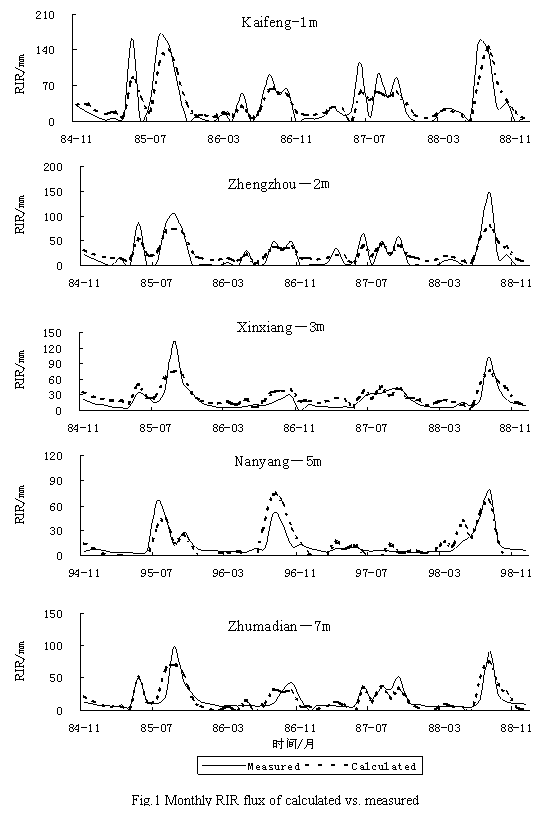
Table 4  Statistical characteristics of error of daily RIRF

 

 

 

References

1.       Wang, D., Zhang, R., Shi, Y., et al., 1995. Foundation of Hydrogeology. Geology Press, Beijing.

2.       Xu, H., 2001. Exploitation and protection of water resources. Geology Press, Beijing.

3.       Zhang, P., Li, R., 1999. The Affecting Factors of Underground Water Supplied by Rain Penetration, Journal of Liaoning University, 26(2):118-122.

4.       Wu, J., Zheng, J., 1999. Model Estimation of Sub-coefficient of Recharge by Rainfall Infiltration, Journal of Hohai University, 27(6):7-11.

5.       Wang, Z., Li, Sh., Xin, X.,et al.,1998. System analysis of precipitation delay recharge, Survey Science and Technology, 4:11-14.

6.       Li, Y., 1997. Lagging distribution of precipitation recharge to phreatic water, Survey Science and Technology, 3:22-26.

7.       Chen Ch., 1998. The weight function method of hysteresis recharge- a method to deal with lagging of precipitation recharge to phreatic water, Hydrogeology and Engineering geology, 6:22-24.

8.       Zhou, M., Jin, M., Wei, Xiu, et al, 2002. Analysis of precipitation recharge using observed data of lysimeter, Geological Science and Technology Information, 21(1):37-40.

  9.       Fang, K., 1994. Uniform design and uniform design table. Science Press, Beijing.