Achievements
GROUNDWATER HEAD FLUCTUATION IN A COASTAL CONFINED AQUIFER OVERLAIN BY A SEMI-PERMEABLE LAYER WITH STORAGE EXTENDING INFINITELY UNDER THE SEA
Li Guohui1 , Li Hailon1, 2 , Xia Yuqiang1 , Guo Qiaona1 , Ren Yakun2,3
1. School of Environmental Studies & (MOE) Biogeology and Environmental Geology Lab, China University of Geosciences, Wuhan 430074, P R China
2. Department of mathematics in
3. Department of mathematics in
Corresponding author. Corresponding address: Dept. of Civil and Env. Enggr,
Abstract: Analytical studies are carried out to investigate groundwater head changes in a coastal aquifer system in response to tidal fluctuations. The system consists of an unconfined aquifer, a leaky confined aquifer and a semi-permeable layer between them. The leaky confined aquifer and its semi-permeable roof extend under the sea infinitely. An exact analytical solution is derived to investigate the influences of both leakage and elastic storage of the semi-permeable layer on the tide-induced groundwater head fluctuation in the semi-confined aquifer. Given the head fluctuation amplitude and phase shift at the coastline, the head fluctuation in inland aquifer behaves exactly the same as that by Li and Jiao [2001b, Advances in Water Resources, p565-573]. Hence the solution analysis focuses on the impacts of the loading effect, the leakage and elastic storage of the roof on the groundwater head fluctuation at the coastline. The head at the coastline fluctuates with an amplitude approximately half of that, and with a phase shift approximately the same as that in the sea sufficiently far from the coastline. The tidal loading on the roof tends to increase the groundwater head fluctuation at the coastline. Leakage from the roof's offshore part enhances the head fluctuation at the coastline. The roof 's elastic storage tends to reinforce the tidal loading effect within the roof and damp the vertical, downward tidal wave propagation due to the direct hydraulic connection of the pore water in the roof with the tidal water at the seabed boundary. The final impact of the roof 's elastic storage is determined by the superposition of these two factors of opposite effects, which leads to a complicated, non-monotone dependence of the head fluctuation at the coastline on the roof 's elastic storage.
Key words: tide, coastal aquifer system, elastic storage, leakance, analytical solution, tidal loading effect
With social and economic development in coastal areas, various coastal hydrogeological, engineering, and environmental problems arise. Solving these problems very often requires studies on the coastal hydrogeological conditions, among which the study on the dynamic relation between seawater and coastal groundwater is significantly important. The water head in coastal aquifer fluctuates in response to the sea tide wave. Since the 1950s, many researchers have studied this phenomenon by analytical or numerical methods. Jacob [1950] derived an exact analytical solution to describe groundwater head in response to sea tide wave in a single confined aquifer extending infinitely landward. Carr and Van der Kamp [1969] studied estimation of aquifer parameters in coastal areas based on equation to describe the tide-induced groundwater fluctuation in a confined aquifer. Van der Kamp [1972] considered groundwater fluctuation in single aquifer with impermeable roof which extends infinitely both seaward and landward. Li and Chen [1991] considered a confined aquifer with an impermeable roof extending a certain distance under the sea. Sun [1997] derived an analytical solution to understand the groundwater response to tidal fluctuation in a single confined aquifer with two-dimensional tidal loading boundary condition of an estuary. Jiao and Tang [1999] discussed the groundwater head fluctuations in the confined aquifer of a coastal multi-layered groundwater system consisting of a confined aquifer, an unconfined aquifer and a semi-permeable layer between them. All layers end at coastline. They ignored the elastic storage of the semi-permeable layer. Based on the work of Li and Chen [1991] and Jiao and Tang [1999], Li and Jiao [2001a] considered a coastal confined aquifer with an semi-permeable roof extending under the sea. They ignored the roof 's elastic storage. Li and Jiao [2001b, 2002] considered both the elastic storage and the leakage of the semi-permeable layer, but all layers of the aquifer system terminate at the coastline.
Based on Li and Jiao [2001a; b], this paper considers a coastal aquifer system consisting of an unconfined aquifer, a leaky confined aquifer, and a semi-permeable layer between them. The leaky confined aquifer and its semi-permeable roof extend infinitely under the sea. Both effects of the elastic storage and the loading efficiency of the semi-permeable layer are taken into account. The mathematic model is given, and the exact analytical solution to the model is derived. The influences of the elastic storage, loading efficiency and leakage of the roof 's offshore portion on the groundwater-head fluctuation in the confined aquifer are discussed.
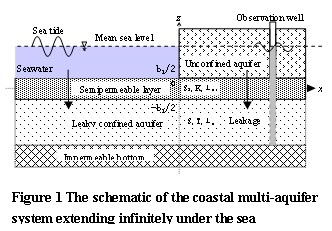
2 Conceptual Model, Mathematical Model and Analytical Solution
Consider a coastal multi-layer aquifer system consisting of a leaky confined aquifer, an unconfined aquifer and a semi-permeable layer between them (Fig. 1). All the layers extend landward infinitely. The bottom of the leaky confined aquifer is impermeable. The leaky confined aquifer and its semi-permeable roof extend infinitely seaward. The unconfined aquifer has a clear-cut vertical boundary with seawater. The coastline is straight. Both the aquifer and the semi-permeable layer are homogeneous, horizontal, and with constant thickness. Following Hantush [1960] and Neuman and Whiterspoon [1969], the flows in the confined aquifer and in the semi-permeable layer are assumed to be horizontal and vertical, respectively. Let the x-axis be positive landward and coincide with the middle line of the semi-permeable layer with its origin at the coastline. Let the z-axis be vertical, positive upward with its origin coincide with the x-axis (see Fig. 1). Following Li and Jiao [1999] and White and Roberts [1994], assume that the shallow unconfined aquifer had a large specific yield which can damp effectively the loading efficiency so that the tidal fluctuation in the unconfined aquifer is negligible compared to that in the confined aquifer. That is to say, the water table of the unconfined aquifer is a constant. According to these assumptions and the theory of Hantush [1960], the mathematical model for this coastal multi-layer aquifer system can be written as the following boundary-value problem. It includes four unknown functions of groundwater-heads in the semi-permeable layer and the confined aquifer including inland and offshore portions.
1) Groundwater flow in the semi-permeable layer:
 (1.1)
(1.1)
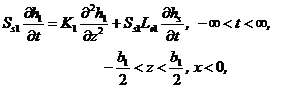 (1.2)
(1.2)
![]() (2.1)
(2.1)
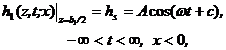 (2.2)
(2.2)

![]() (3)where
(3)where
![]() denotes the hydraulic head [L] of
the groundwater in the semi-permeable layer at the location
denotes the hydraulic head [L] of
the groundwater in the semi-permeable layer at the location ![]() and time
and time ![]() ;
; ![]() and
and ![]() are the specific storativity [L-1]
and vertical hydraulic conductivity [LT2] of the semi-permeable
layer, respectively;
are the specific storativity [L-1]
and vertical hydraulic conductivity [LT2] of the semi-permeable
layer, respectively; ![]() is the loading efficiency of the
semi-permeable layer;
is the loading efficiency of the
semi-permeable layer; ![]() is the thickness of the
semi-permeable layer [L],
is the thickness of the
semi-permeable layer [L], ![]() is the constant
water table of the unconfined aquifer overlying the semi-permeable layer [L].
The water table surface is chosen to be the datum of hydraulic-head so that
is the constant
water table of the unconfined aquifer overlying the semi-permeable layer [L].
The water table surface is chosen to be the datum of hydraulic-head so that ![]() , and
, and ![]() is the hydraulic head [L] of the
main aquifer at the instant
is the hydraulic head [L] of the
main aquifer at the instant ![]() and location
and location ![]() .
.
2) Groundwater flow in confined aquifer control layer:
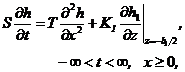 (4.1)
(4.1)
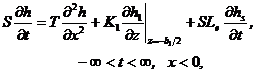 (4.2)
(4.2)
![]()
![]() (5.1)
(5.1)
![]()
![]() (5.2)
(5.2)
![]()
![]() (6)
(6)
![]()
![]() (7)
(7)
Here ![]() and
and ![]() are the storativity
(dimensionless) and the transmissivity [L2T-1] of the
main aquifer, respectively;
are the storativity
(dimensionless) and the transmissivity [L2T-1] of the
main aquifer, respectively; ![]() is the phase shift
(dimensionless); and
is the phase shift
(dimensionless); and ![]() is the angular velocity [T-1]
of tide and equals
is the angular velocity [T-1]
of tide and equals ![]() , where
, where ![]() is the tidal period [T].
is the tidal period [T].
The derivation of the solutions ![]() and
and ![]() to the boundary value system
(1)-(7) is presented in detail in the appendix A. The analysis will focus on
the groundwater-head
to the boundary value system
(1)-(7) is presented in detail in the appendix A. The analysis will focus on
the groundwater-head ![]() in the main aquifer due to space
limitation. Hence, only the expression of
in the main aquifer due to space
limitation. Hence, only the expression of ![]() will be given here. Details about
will be given here. Details about
![]() are presented in the Appendix A.
For convenience of discussion, three parameters are introduced as in Li and
Jiao [2002]. They are the main aquifer's tidal propagation parameter
are presented in the Appendix A.
For convenience of discussion, three parameters are introduced as in Li and
Jiao [2002]. They are the main aquifer's tidal propagation parameter ![]() [L-1], the buffer
capacity
[L-1], the buffer
capacity ![]() (dimensionless) and the dimensionless
leakage
(dimensionless) and the dimensionless
leakage ![]() (dimensionless):
(dimensionless):
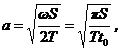 (8)
(8)
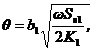 (9)
(9)
![]() (10)
(10)
where ![]() is the specific leakage of the
semi-permeable layer. Then, the solution
is the specific leakage of the
semi-permeable layer. Then, the solution ![]() can be written as
can be written as
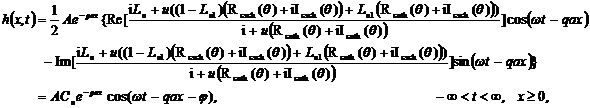 (11.1)
(11.1)
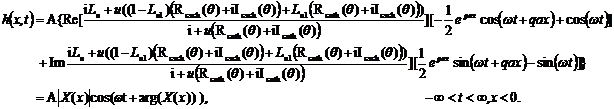 (11.2)
(11.2)
where ![]() and
and ![]() are dimensionless constants
defined as
are dimensionless constants
defined as
![]() (12.1)
(12.1)
![]() (12.2)
(12.2)
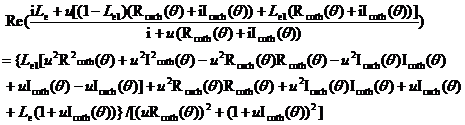 (12.3)
(12.3)
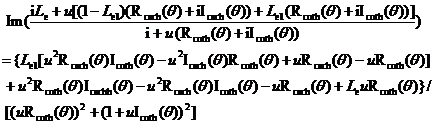 (12.4)
(12.4)
![]() (12.5)
(12.5)
![]() (12.6)
(12.6)
in which the function ![]() and
and ![]() are given by
are given by
![]() (13.1)
(13.1)
![]() (13.2)
(13.2)
![]() (13.3)
(13.3)
![]() (13.4)
(13.4)
![]() (13.5)
(13.5)
![]() (13.6)
(13.6)
3 Discussion
Equations (11.1) and (11.2) are the solutions for the groundwater heads in inland and offshore parts of the main aquifer, respectively.
When ![]() , or equivalently
, or equivalently![]() , from (13.1) and (13.2), one has
, from (13.1) and (13.2), one has
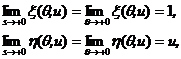 (14)
(14)
Substituting (14) back into (12.1), (12.2) yields
 (15)
(15)
![]() (16)
(16)
Using (16) and (A17.1)-(A17.2.2), one obtains
 (17.1)
(17.1)
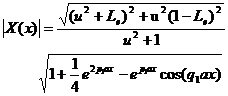 (17.2)
(17.2)
![]() (18.1)
(18.1)
![]() (18.2)
(18.2)
Substituting (17.1)-(18.2) back into (11.1) and (11.2), it is follows that
 (19.1)
(19.1)
 (19.2)
(19.2)
This solution is used to describe this coastal aquifer system ignoring the roof 's elastic storage.
When![]() ,
,
![]() (20)
(20)
Using (20) and (17.1)- (17.2.2), one obtains
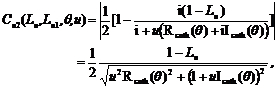 (21.1)
(21.1)
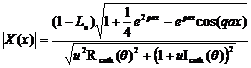 (21.2)
(21.2)
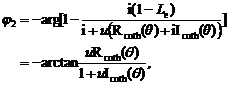 (22.1)
(22.1)
![]() (22.2)
(22.2)
It is follows that
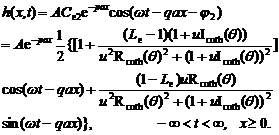 (23.1)
(23.1)
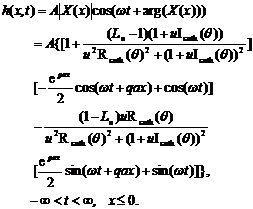 (23.2)
(23.2)
This is a new solution. For aquifer systems with semi-permeable layer composed of thick, soft sedimentary materials, the loading efficiency is always great between 0.8 and 1.0. So this solution has the practical significance.
Comparisons
of the groundwater head amplitude and phase shift in the confined aquifer
between in the sea infinitely seaward (![]() ) and at coastline (
) and at coastline (![]() ) are made. To a fixed location
) are made. To a fixed location![]() ,
, ![]() and
and ![]() are the groundwater head
amplitude in confined aquifer of the landward proportion and seaward proportion
respectively.
are the groundwater head
amplitude in confined aquifer of the landward proportion and seaward proportion
respectively. ![]() and
and ![]() are the groundwater head phase
shift of the landward proportion and seaward proportion respectively. Basing on
(11.1) and (11.2), yields
are the groundwater head phase
shift of the landward proportion and seaward proportion respectively. Basing on
(11.1) and (11.2), yields
![]() (24)
(24)
Comparing (24) and (11.1) - (11.2), leads
![]()
![]()
![]()
![]() (25)
(25)
![]()
![]()
![]()
![]() (26)
(26)
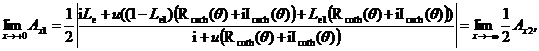 (27)
(27)
![]() (28)
(28)
(27) and (28) demonstrate that the head fluctuation
amplitude at coastline (![]() ) is half of that in the sea
infinitely far from the coastline, but the phase shift at the coastline is the
same as that in the sea infinitely far from the coastline.
) is half of that in the sea
infinitely far from the coastline, but the phase shift at the coastline is the
same as that in the sea infinitely far from the coastline.
3.2 The influence of loading efficiency, leakage and buffer capacity of the semi-permeable on groundwater-head fluctuation amplitude at the coastline
From
equations (8)-(11.2),(12.1)-(12.6),(13.1)-(13.6), it can be seen that five
important parameters: the
dimensionless leakances of the semi-permeable layer, the buffer capacity of the
semi-permeable layer, the confined aquifer's tidal propagation
parameter, and loading efficiencies of the semi-permeable layer and leaky
confined layer, respectively are involved in
the model. For the need of discussion, the values of ![]() ,
, ![]() and
and ![]() corresponding to some case
studies are calculated by Eqs. (8)-(10) for the semidiurnal sea tide whose
angular velocity
corresponding to some case
studies are calculated by Eqs. (8)-(10) for the semidiurnal sea tide whose
angular velocity ![]() . Based on the data presented in
Li and Jiao [2001b] (see Table 1), the discussion ranges of the parameters will
be chosen 0.0-25.0 for
. Based on the data presented in
Li and Jiao [2001b] (see Table 1), the discussion ranges of the parameters will
be chosen 0.0-25.0 for ![]() , 0.0-20.0 for
, 0.0-20.0 for ![]() , 0.0-1.0 for
, 0.0-1.0 for ![]() , and 0.8-1.0 for
, and 0.8-1.0 for ![]() .
.
Figure 2
describes that the amplitude of groundwater head fluctuation at coast line
changes with buffer capacity for different loading efficiency and different leakances of the semi-permeable layer.
Let the confined aquifer's loading efficiency be a mean value 0.5. The
semi-permeable layer's loading efficiency takes two groups of values 0.8 and
1.0, Each group has four curves of leakance (![]() =0.1,1.0,5.0,20 ).
=0.1,1.0,5.0,20 ).
In Fig 2,
when ![]() the amplitude coefficient
increases with the leakage. For
the amplitude coefficient
increases with the leakage. For ![]() , when the buffer capacity is
small, the amplitude reduces quickly for a small distance; subsequently, it
increases gradually to a certain constant. The physical mechanism of the buffer
capacity results in it according to Eq. (9). Small buffer capacity implies that
the
elastic storage of the leaky layer is
very small, and the semi-permeable layer can not counteract the large leakage.
Thus minimum amplitude is
, when the buffer capacity is
small, the amplitude reduces quickly for a small distance; subsequently, it
increases gradually to a certain constant. The physical mechanism of the buffer
capacity results in it according to Eq. (9). Small buffer capacity implies that
the
elastic storage of the leaky layer is
very small, and the semi-permeable layer can not counteract the large leakage.
Thus minimum amplitude is 
 caused. Meanwhile, the roof 's ability of storing
water enhances with the buffer capacity increases, then, weakens the interference
induced by tide wave, and amplitude enhances. When the buffer capacity large
enough to counteract the leakage, the amplitude will insensitive to the buffer
capacity and intends to a certain constant. When
caused. Meanwhile, the roof 's ability of storing
water enhances with the buffer capacity increases, then, weakens the interference
induced by tide wave, and amplitude enhances. When the buffer capacity large
enough to counteract the leakage, the amplitude will insensitive to the buffer
capacity and intends to a certain constant. When ![]() , the amplitude raises quickly
first, and subsequently increases gradually to a constant. The reason for this
behavior is that the change of groundwater head is mainly dominated by leakage
from seaward when the leakage is small. Leakances from seaward enhance the
change, while leakances from inland weaken it (Li and Jiao [2001a]). So for large leakage, large buffer
capacity enhances the amplitude while small buffer capacity behaves as a
damping factor. The behaviors of curves
, the amplitude raises quickly
first, and subsequently increases gradually to a constant. The reason for this
behavior is that the change of groundwater head is mainly dominated by leakage
from seaward when the leakage is small. Leakances from seaward enhance the
change, while leakances from inland weaken it (Li and Jiao [2001a]). So for large leakage, large buffer
capacity enhances the amplitude while small buffer capacity behaves as a
damping factor. The behaviors of curves ![]() are similar to that of
are similar to that of ![]() . Fig 2 also implies that for
the same leakage, larger semi-permeable layer's loading efficiency induces
larger amplitude.
. Fig 2 also implies that for
the same leakage, larger semi-permeable layer's loading efficiency induces
larger amplitude.
The tidal loading on the roof tend to increases the groundwater head fluctuation at the coastline. Leakage from the roof 's offshore part enhances the head fluctuation at the coastline. The roof 's elastic storage tends to reinforce the tidal loading effect within the roof and damp the vertical, downward tidal wave propagation due to the direct hydraulic connection of the pore water in the roof with the tidal water at the seabed boundary. The final impact of the roof 's elastic storage is determined by the superposition of these two factors of opposite effects, which leads to a complicated, non-monotone dependence of the head fluctuation at the coastline on the roof 's elastic storage.
4 Conclusion
Analytical studies are carried out to investigate groundwater head changes in a coastal aquifer system in response to tidal fluctuations. The system consists of an unconfined aquifer, a leaky confined aquifer and a semi-permeable layer between them. The leaky confined aquifer and its semi-permeable roof extend under the sea infinitely. An exact analytical solution is derived to investigate the influences of both leakage and elastic storage of the semi-permeable roof on the tide-induced groundwater head fluctuation in the semi-confined aquifer. Given the head fluctuation amplitude and phase shift at the coastline, the head fluctuation in inland aquifer behaves exactly the same as that by Li and Jiao [2001b]. Hence the solution analysis focuses on the impacts of the loading efficiency, the leakage and elastic storage of the roof on the groundwater head fluctuation at the coastline. The head at the coastline fluctuates with an amplitude approximately half of that, and with a phase shift approximately the same as that in the sea sufficiently far from the coastline. The tidal loading on the roof tend to increases the groundwater head fluctuation at the coastline. Leakage from the roof 's offshore part enhances the head fluctuation at the coastline. The roof 's elastic storage tends to reinforce the tidal loading effect within the roof and damp the vertical, downward tidal wave propagation due to the direct hydraulic connection of the pore water in the roof with the tidal water at the seabed boundary. The final impact of the roof 's elastic storage is determined by the superposition of these two factors of opposite effects, which leads to a complicated, non-monotone dependence of the head fluctuation at the coastline on the roof 's elastic storage.
Appendix
To simplify the calculation, let the sea water head ![]() noting
noting ![]() then
then
![]() , (A1)
, (A1)
Analogously we can write
![]() (A2)
(A2)
Where ![]() and
and ![]() are complex functions, Re
denotes the real part of the followed complex expression, and
are complex functions, Re
denotes the real part of the followed complex expression, and ![]() . Substituting (A.1) back into
(1.1)-(3), yields
. Substituting (A.1) back into
(1.1)-(3), yields
![]() (A3.1)
(A3.1)
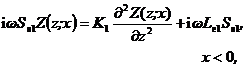 (A3.2)
(A3.2)
![]() (A4.1)
(A4.1)
![]() (A4.2)
(A4.2)
![]()
![]() (A5)
(A5)
then the solutions to (A3.1)-(A5) are:
![]() (A6.1)
(A6.1)
![]() (A6.2)
(A6.2)
Where
![]() (A6.1.1)
(A6.1.1)
![]() (A6.1.2)
(A6.1.2)
![]() (A6.2.1)
(A6.2.1)
![]() (A6.2.2)
(A6.2.2)
After substitution (A6.1.1)-(A6.2.2)
back to (A6.1) and (A6.2) and simplification, ![]() can be written as following
can be written as following
![]() (A6.3)
(A6.3) 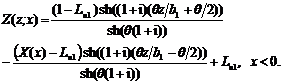 (A6.4)
Using (A6.3) and (A6.4), one obtains:
(A6.4)
Using (A6.3) and (A6.4), one obtains:
 (A7.1)
(A7.1)
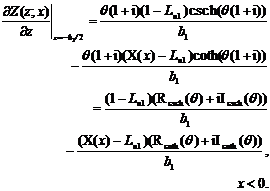 (A7.2)
(A7.2)
Substituting Eqs. (A2), (A7.1) and (A7.2) back into Eqs. (4.1)-(7), yields
![]() (A8.1)
(A8.1)
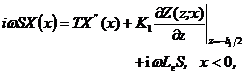 (A8.2)
(A8.2)
![]() (A9)
(A9)
![]() (A10)
(A10)
![]() (A11)
(A11)
![]() (A12)
(A12)
The solution of (A8.1)-(A12) is
![]() (A13.1)
(A13.1)

![]() (A13.2)
(A13.2)
where
![]() (A13.1.1)
(A13.1.1)
![]() (A13.1.2)
(A13.1.2)
![]() (A13.2.1)
(A13.2.1)
![]() (A13.2.2)
(A13.2.2)
Substitute (A6.3), (A6.4), (A13.1) and (A13.2.2) back into (A1) and (A2) lead to the solution to (1.1)-(3). The expression of the solution is very complex, so it is not given here. Substituting (A13.1) and (A13.2.2) back into (A2) lead to the solution (11.1)-(11.2) to (4.1)-(7).
Reference
[1] Carr, P. A. and Van der Kamp, G.. 1969. Determining aquifer characteristics by the tidal methods. Water Resource Research; 5(5), 1023-1031.
[2] Hantush MS. 1960. Modification of the theory of leaky aquifers. J Geophys Research; 65(11): 3713-6.
[3] Jacob CE. 1950. Flow of groundwater. In: Rouse H,
editor. Engineering hydraulics.
[4] J. J. Jiao. and Tang Z. 1999. An analytical solution of groundwater response to tidal fluctuation in a leaky confined aquifer. Water Resources Research; 35(3): 747-51.
[5] Li, G. and Chen, C. 1991. Determining the length of confined aquifer roof extending under the sea by the tidal method. J. Hydrol.; 123, 97-104.
[6] Li, H. and J. J. Jiao. 2001a. Tide-induced groundwater fluctuation in a coastal leaky confined aquifer system extending under the sea. Water Resources Research; 37(5):1165-71.
[7] Li, H. and J. J. Jiao. 2001b. Analytical studies of groundwater-head fluctuation in a coastal confined aquifer overlain by a semi-permeable layer with storage. Advances in Water Resources; 565-573.
[8] Li, H. and J. J. Jiao. 2002. Analytical solutions of tidal groundwater flow in coastal two-aquifer system. Advances in Water Resources; 417-426.
[9] Neuman SP, Witherspoon PA. 1969. Theory of flow in a confined two aquifer system. Water Resources Res; 5(4): 803-16.
[10] Sun, H., 1997. A two-dimensional analytical solution of groundwater response to tidal loading in an estuary. Water Resource Research; 33(6): 1429-1435.
[11] Van der Kamp, G. 1972. Tidal fluctuations in a confined aquifer extending under the sea. Proc. Int. Geol. Congr.; 24, 101-106.
[12] White JK, Roberts TOL. 1994. The significance of
groundwater-tidal fluctuations. In: Wilkinson WB, editor. Proceedings of the
International Conference Organized by the Institution of Civil Engineers,
Table1
the range of ![]() and
and ![]()
|
Confined aquifer |
Semi-permeable layer |
Model parameters | ||||||
|
|
|
(m) |
(md-1) |
|
(m) |
(m-1) |
|
|
|
108 |
0.000036 |
14 |
0.013 |
0.001 |
4 |
0.001423 |
7.433941 |
1.366861 |
|
158 |
0.000045 |
14 |
0.013 |
NA |
4 |
0.001315 |
5.947153 |
NA |
|
114 |
0.00003 |
14 |
0.013 |
0.0035 |
4 |
0.001264 |
8.920729 |
2.557162 |
|
1624 |
0.000112 |
28 |
0.0016 |
0.003 |
9.1 |
0.000647 |
0.12927 |
10.17858 |
|
1624 |
0.000112 |
28 |
0.0016 |
0.012 |
15.2 |
0.000647 |
0.077392 |
26.30985 |
|
7.31 |
0.000098 |
6.1 |
0.0082 |
0.004 |
3 |
0.009022 |
2.296703 |
2.980915 |
|
733 |
0.00009 |
16 |
0.0021 |
0.0005 |
13.1 |
0.000863 |
0.146671 |
4.35188 |
Note: "NA" means that data are not available.




