Achievements
JC METHOD FOR UNCERTAINTY ANALYSIS IN EVALUATION OF GROUNDWATER ALLOWABLE WITHDRAWAL
Shu Long-cang, Liu Pei-gui, Dong Gui-ming, Basil Iro Ongor
(State Key Lab of Hydrology-Water
Resources and Hydraulic Engineering, Hohai
University, Nanjing
210098,
Abstract: Calculation
of groundwater allowable withdrawal is the key task of evaluating groundwater
resources. However, the precise amount of groundwater allowable withdrawal is
under uncertainties associated with the real values of the parameters and
simplification of mathematical model. The traditional deterministic method of
water balance evaluation has a number of limitations, and the risk associated
with the results is overwhelming. In this study, JC method which is an
improvement method of first-order second-moment is used in determining the
groundwater allowable withdrawal for the well field in
Jining City, Shandong
Province,
Key words: groundwater allowable withdrawal; uncertainty analysis; JC method; traditional deterministic model; groundwater resources
Introduction
Groundwater is an important water supply source due to its wide distribution, good water quality and the fact that it is not easily polluted. It is virtually a nature resource and plays a vital role in the society, economy and ecology development. However, with the population increasing and the city size broadening coupled with agricultural and industrial growth, the over exploitation of groundwater has resulted in some critical problems, such as decline of water table level, land subsidence, cone of depression formation, seawater intrusion, etc. Other negative effects that may arise are depletion of stream flow and drying of wetlands (Shu & Chen, 2003). To combat these situations, much emphasis should be put on the groundwater resource evaluation, especially the estimation of groundwater allowable withdrawal (GWAW), which is traditionally evaluated by use of deterministic model. Like most other systems, groundwater system is uncertain in essence. Accordingly, there exist a lot of uncertain factors in the process of determining the GWAW. Based on the sources of influencing factors, uncertainties are divided into two parts: objective uncertainties and subjective uncertainties (Shu & Zhu, 2000). The former is mainly concerned with the values of parameters, source and sink items, through time and space. The groundwater level and groundwater quality are random variables changing with time and in space. This is well illustrated by the hydrogeological parameters, whose real values are virtually impossible to obtain at the research area by using pumping tests, and quite often the average value obtained from the limited number of pumping tests is considered as the true value of the whole research area.
Subjective uncertainties in groundwater resource evaluation are introduced: developing numerical simulation model of groundwater flow, and using the different mathematical models in the same study area, and collecting the data through observation or measurement. Quite often, due to lack of adequate data, groundwater flow model development entails simplification of the actual hydrogeological conditions. In some cases, most aquifers are heterogeneous and anisotropic, but are often simplified as heterogeneous and isotropic, or even homogeneous and isotropic, which introduces uncertainties into the GWAW determination inevitably. Moreover, adoption of uncorrected mathematical model in analyzing hydrogeological conditions with limited information also introduces more uncertainties. The following case study on a karstic aquifer is a good example of interpretation the uncertainties. Under the condition of limited data, and if the steady state model is applied to simulate groundwater flow, the calibration residual is normally big in the case of the mine drainage in the karsts aquifer. This real condition proves that unsteady flow model should be applied to predict the mine drainage (Lin & Liao, 1992). Observation and measurement during data acquisitions also immensely introduce uncertainties.
In general, there exist a number of uncertainties in groundwater systems, which directly or indirectly affect the reliability of GWAW and the sustainable management of well field. The traditional deterministic model can not take uncertainties into consideration very well; hence, it is greatly necessary to establish a new method to deal with uncertainties in order to design optimal and sustainable groundwater exploitation strategies.
Uncertainty is closely related to risk, and the reliability and credibility of the GWAW can be improved by combining the risk analysis method with uncertainties analysis. Presently First-Order Second-Moment (FOSM) method is the most widely used technique in engineering application, partly due to its simplicity (Jang Y S, et al.1994; Shreedhar & Vincent, 2003). However, this method suffers from a number of limitations. The main problem arises from the linearization in the mean values of the input variables and inconsideration of the different distributed model of random variable. An improvement of the FOSM is JC method which is illustrated in this paper in assessing the reliability of GWAW. First, the JC method is described, and then an application example is presented. Finally, discussion and conclusion are made.
JC METHOD
Principle of FOSM method
For the sake of generality, consider a function of several random variables:
![]() (1)
(1)
Where![]() represents the random variable,
the indices 1, 2, . , n respectively indicate the type of influencing factors.
represents the random variable,
the indices 1, 2, . , n respectively indicate the type of influencing factors.
According to
the ![]() is expanded about the point of
is expanded about the point of![]() , and yields the following
expressions in the first order (Zhao, 1996; Ma, 2004):
, and yields the following
expressions in the first order (Zhao, 1996; Ma, 2004):
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
The reliability index ![]() is expressed as:
is expressed as:
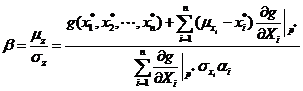
(5)
If the point of ![]() is chosen as the design check
point, Eq. (5) is then transformed into:
is chosen as the design check
point, Eq. (5) is then transformed into:
![]() (6)
(6)
Where ![]() is the sensitivity index, given
by:
is the sensitivity index, given
by:
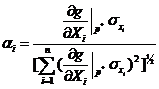 (7)
(7)
With the iterative design method, the values of ![]() and reliability
and reliability ![]() can be obtained from the
equation:
can be obtained from the
equation:
![]() (8)
(8)
Principle of JC method
Despite the
simplicity of FOSM, the method considers all of the random variables in the
function as normally distributed, which is not the
case. One possible way to improve the accuracy of the approximation is
to use higher order from the
An improvement method of JC method aims at overcoming the problem based on the following premises. First, it transforms the non-normal distribution of random variables to the normal distribution in the design check point instead of mean values, which meets the two conditions simultaneously: the values of the probability density function (PDF) should be the same as the equivalent normal distribution in the point of failure. Cumulative density function (CDF) should also satisfy the limiting condition (Fig.1). The two equations are written as:
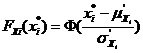 (9)
(9)
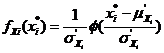 (10)
(10)
Where
![]() is the given CDF of the random
variable
is the given CDF of the random
variable![]() ,
, ![]() is the given PDF of the random
variable
is the given PDF of the random
variable![]() ,
, ![]() is the equivalent mean value,
is the equivalent mean value, ![]() is the equivalent standard
deviation.
is the equivalent standard
deviation.
Then the given means and standard deviations are replaced with the means and standard deviations of the equivalent normal distribution. Finally, it employs a First-Order Taylor series expansion to combine model sensitivity with uncertainty and use the FOSM method to compute the reliability index.
Application example
Jining City is
located in the southwest of
![]() (11) Where
(11) Where ![]() represents the head
difference between deep confined aquifer and shallow aquifer,
represents the head
difference between deep confined aquifer and shallow aquifer, ![]() is
the coefficient of leakage,
is
the coefficient of leakage, ![]() is the gradient,
is the gradient, ![]() is the transmissivity,
is the transmissivity, ![]() is the groundwater pumping
rate,
is the groundwater pumping
rate, ![]() is the storage coefficient of the aquifer,
F and
is the storage coefficient of the aquifer,
F and ![]() are the distribution area and the
perimeter of the aquifer respectively,
are the distribution area and the
perimeter of the aquifer respectively, ![]() is the average variation of the
water level within the time of
is the average variation of the
water level within the time of ![]() .
.
Determination of random variables
Sensitivity
analysis (SA) is closely linked to uncertainty analysis, which aims at
quantitative assessment of the overall uncertainty associated with the response
as a result of uncertainties in the model input. The
sensitivity analysis results can provide a better understanding of how the
model response to variables changes in the inputs.
The four variables ![]() are chosen as the main
random variables in the study area (Table 1). The coefficient of leakage
are chosen as the main
random variables in the study area (Table 1). The coefficient of leakage ![]() and the transmissivity
and the transmissivity ![]() are both considered as lognormal
distribution (Law, 1944; Li & Shu, 2005). Both
are both considered as lognormal
distribution (Law, 1944; Li & Shu, 2005). Both![]() and
and ![]() are assumed to be normal
distribution. Using the statistical analysis, the mean and standard deviation
of each random variable can be obtained from pumping tests (Table 2).
are assumed to be normal
distribution. Using the statistical analysis, the mean and standard deviation
of each random variable can be obtained from pumping tests (Table 2).
Results and discussions
The groundwater level above the top of aquifer is forty-five meters on
average, and assuming that the well field is to be run for about twenty years,
then according to the definition of GWAW, the annual average allowable drawdown
is 2.25 meters in the study area. Owing to the
limitations of traditional method, the effect of uncertainties on the calculation
of GWAW in
GWAW obtained from the traditional deterministic model is 14.68×104 m3/d, but its corresponding reliability based on JC method is only 64.80%, hence the occurrence of risk as hydrogeological problems is still 35.20%. Presently, the well field reliability under traditional method of GWAW shows that whereas the groundwater abstraction was 14.35×104 m3/d, GWAW was 14.68×104 m3/d in 1987, yet the groundwater level was still decreasing. This reflects the omission of uncertainties effects, and proves the great influence of uncertainties in the groundwater evaluation results obtained from the traditional deterministic method. The JC method provides an effective method to deal with uncertainties in the process of determining GWAW and makes up the shortcomings of the deterministic model. With the JC method, the different GWAW and corresponding reliabilities can be achieved, with the GWAW of 100% reliability being 8.26×104 m3/d (Table3).
Effects of the distributions of random variables
For a given mean and standard deviation, two different PDF are assumed for the transmissivity and the coefficient of leakage i.e. logarithmic normal and normal. At higher reliabilities, the computed results based on JC method become closer for these two distributions (Fig.2).
Effects of the means of random variables
Different means are obtained from different number of samples, and by changing the means of transmissivity and the coefficient of leakage by 10%, the effect of means is assessed (Fig.3).
Figure 2 and Figure 3 illustrate that the type of PDF for the transmissivity and the coefficient of leakage is not the most influential factor in the study area; hence a normal distribution can be replaced with lognormal distributions in this well field. However more work on groundwater exploration and investigation in the study area should be done in order to improve the reliability of groundwater resource evaluation.
Conclusions
In this paper, JC method is presented to deal with uncertainties that exist in the groundwater system and assess the reliability of GWAW, which the widely used traditional deterministic method can not effectively deal with, given the spatial distribution of main parameters. Compared with the GWAW of 14.68×104 m3/d determined by the traditional deterministic method, the result obtained from the JC method has higher reliability due to uncertainties considerations. Hence, it minimizes the risk of ecological, environmental and hydrogeological problems generated by the overdraft of groundwater resources to a certain degree. It also makes up for the limitations of the deterministic model by establishing random mathematical model. Results from the study area illustrate that the means of random variables are the most influencing factors, as such more hydrogeological studies should emphasis in them
Uncertainty analysis and risk analysis present an essential new research field in groundwater resources evaluation, management and sustainable development.
Acknowledgement
The study is supported by the State Key Lab of Hydrology-Water Resources and Hydraulic Engineering of Hohai University. Thanks also to Jining Bureau of Water Resource, Shandong Province of China for their collaboration.
References
[1] Shu Long-cang, Chen Xun-hong. (2003) Impact of Groundwater Pumping on Stream Flow Depletion. Journal of Hydraulic Engineering. 2, 112-116.
[2] Shu Long-cang & Zhu Yuan-sheng. (2000) Uncertainties Analysis of Groundwater Resource Evaluation. Hydrogeology & Engineering Geology. 6, 6-8.
[3] Lin Xue-yue, Liao Zi-sheng. Importance of Hydrogeological Basic Work in the Groundwater Model Research. Hydrogeology & Engineering Geology.1992, 19 (1):6-8.
[4] Shu Long-cang, Sun Qing-yi, Zhu Yuan-sheng, & Peng Xu-min. (2000) Risk Analysis of Groundwater Allowable Withdrawal Evaluation. Journal of Hydraulic Engineering. 3, 77-81.
[5] Jang Y S, Sitar N & Kiureghian A D. (1994) Reliability Analysis of Contaminant Transport in Saturated Porous Media. Water Resource Res. 30(8), 2435~2448.
[6] Shreedhar Maskey & Vincent Guinot. (2003) Improved First-Order Second Moment Method for Uncertainty Estimation in Flood Forecasting. Hydrological sciences-journal-des sciences hydrologiques. 48(2), 183-196.
[7] Ma Rong-yong. (2004) The Methods And Application of
Risk Analysis in Earth--Rockfill Dam. Science publication,
[8] Zhao Guo-fan. (1996) Reliability Theory and Its
Applications for Engineering Structures. Dalian
university of technology press,
[9] Shu Long-cang, Sun Qingyi, Peng Xunmin & Wen
Zhonghui. (2001) Analysis on Influence Factors of Sustainable Groundwater
Development in Jining City, Shandong
Province,
[10] Law, J. (1944) Statistical Approach to the Interstitial Heterogeneity of Sand Reservoirs.Trans. AIME. 155:202-222.
[11]
Li
Wei & Shu Long-cang. (2005) Probability Distribution Characteristics of
Vertical Hydraulic Conductivity in Substrate of
Figure Caption:
Figure 1. Equivalent normal distribution of JC method
Figure 2. Effect of different PDF: log normal and normal
Figure 3. Effect of the given means
Table1 Results of sensitivity analysis
|
Parameters |
|
|
|
|
|
|
Values |
0.59 |
0.59 |
0.41 |
0.41 |
0.003 |
Table2 Mean and standard deviation of each random variable
|
statistic |
|
|
|
|
|
|
12.5 |
0.000215 |
1166.35 |
0.0024 |
|
|
1.443376 |
0.000049 |
264.732048 |
0.000808 |
Table3 Results of JC method
|
Exploitation |
14.68 |
14.21 |
13.18 |
11.84 |
8.26 |
|
Reliability (%) |
64.80 |
70.00 |
80.00 |
90.00 |
100.00 |
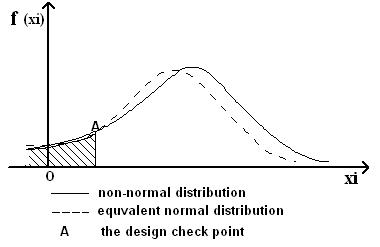
Fig.1.
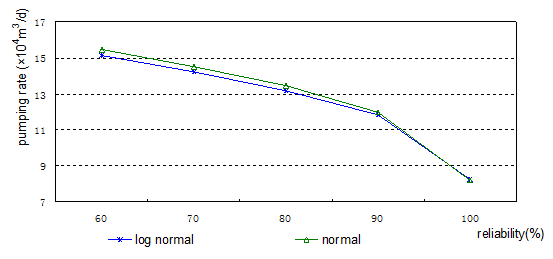
Fig.2.
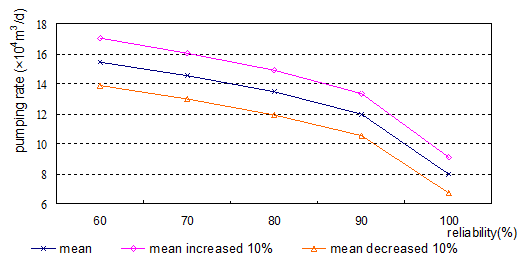
Fig.3.




