Evolutional Rules of Regional Groundwater System
EXPERIMENTAL STUDY OF GROUNDWATER NON-DARCY FLOW IN A PARALLEL GLASS PLATE FRACTURE
QIAN Jiazhong,YE Hao,WANG Jiaquan,ZHAO Weidong
School of Natural Resources and
Environmental Engineering, Hefei University of Technology,
Abstract: Mechanism study of groundwater flow in a single fracture is a basis to describe contaminant transport in the media of fractures. It is of important significance to study the storages of oil, gas and nuclear deposits. In this paper, the simulated experiment is done to study the relation between the average velocity and hydraulic gradient in a parallel glass plate fracture. The invalidation of Darcy’s Law is experimented. A non-Darcy flow equation is established. The relation of Reynolds number, average velocity and hydraulic radium is analyzed. And a critical Reynolds number for determining groundwater flow type is discussed. The critical Reynolds number should be less than 14.9259 under the experimental conditions.
Key Words: groundwater; non-Darcy flow; critical Reynolds number; parallel glass plate fracture; experimental study
1 Introduction
Ground water movement in naturally fractured media is highly complex due to the strongly varying velocity fields. There have been studies about groundwater movement in natural fractured media, but they are almost treated by using some form of the seepage equation based on Darcy’s Law, or by using related approaches, which is based on the same assumptions. Based on the assumptions, double porous media or equivalent porous media models are employed to simulated groundwater flow in fracture karst media. However, recent years, as demonstrated frequently in the literature, the above-mentioned approaches often fail to capture groundwater flow in the fracture systems. This failure is most clearly evidenced by the finding of non-Darcy’s behavior in fractured media. The references just mentioned show that it is essential to study the mechanism of flow in fractures and to establish the correct conceptual model [4-8].
Mechanism of
groundwater water flow in a single fracture is studied for a long time. Early
in 1951, Russian scholar Lomize (1951)[9] studied the movement of
groundwater in a single smooth fracture, and Reynolds number suggested as an
index of distinguishing flow type. The critical Reynolds number is 600 from the
laminar to the turbulent flow. However, Louis(1969) studied the single rough
fracture, and got a critical Reynolds number which is 2300. Romm[10]
studied the cases of tiny fractures(10~100![]() ) and infinitesimal
fractures(0.25~4.3
) and infinitesimal
fractures(0.25~4.3![]() ), and suggested that the cube law
is always tenable if only the width of fractures is more than 0.2
), and suggested that the cube law
is always tenable if only the width of fractures is more than 0.2![]() . Through experiment study, Su
Baoyu[11]and WANG Yuan et al[12] suggested that natural
fracture seepage still obeys the cube law when the flow fype is laminar flow,
but through armor plate fracture experiment, Xu Guangxiang et al. considered
that rough fracture seepage doesn’t obey the cube law, instead, it obeys the
super-cube law or the hypo-cube law. Furthermore, Sun Fenggen et al[14],Qian
Jiazhong et al.[15] proved that fracture water appears non-Darcy
behavior under laboratory condition by a single fracture study.
. Through experiment study, Su
Baoyu[11]and WANG Yuan et al[12] suggested that natural
fracture seepage still obeys the cube law when the flow fype is laminar flow,
but through armor plate fracture experiment, Xu Guangxiang et al. considered
that rough fracture seepage doesn’t obey the cube law, instead, it obeys the
super-cube law or the hypo-cube law. Furthermore, Sun Fenggen et al[14],Qian
Jiazhong et al.[15] proved that fracture water appears non-Darcy
behavior under laboratory condition by a single fracture study.
The main purpose of the Experiment is studying the mechanism of groundwater seepage under different conditions in a parallel glass plate fracture, validating the traditional Darcy law and the corresponding cube law and discussing the Reynolds number which is used to judge flow form in a single fracture.
2 Experiment of Parallel Glass Plate Fracture
Figure 1 is a schematic diagram of the experimenter. The structure dimensions are labeled in fig 1(unit: cm). The model is made of organic glass plate, and the width of fracture can be adjusted so as to do more experiments with different degrees of hatch. To keep hydraulic pressure stabilization of infall, we take perch water tank to recharge the fracture. A LZJ-6 flowmeter is installed in upstream of the fracture. And an overfall slot in water tank is installed for stable recharge to the fracture. Another LZJ-6 flowmeter is installed in the downstream of the fracture to keep the same flow in the fracture.Repeat the above steps by adjusting the width of fracture and controlling different water levels, we can do many experiments to study the movement rules of fracture water with different widths and different water levels.
Experimental approach: the experiment use the LZJ-6 flowmeter to measure stable flux with an error less than 2.5 %, and use pressure meter to measure water level with an error between negative 5 mm and positive 5 mm.
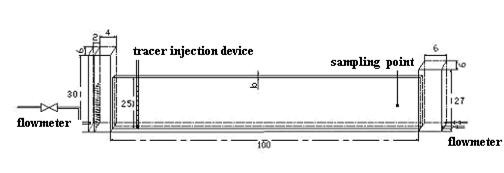
Fig. 1 Sketch map of single fracture flow experiment
3 The Analysis of Experimental Results
3.1 The experiment of the Darcy law’s
To test applicability of the Darcy law, we calculate the average velocity of flow in the fracture in terms of the data of the water level、the widths of fracture、the length of flow and stable flux. The data of the hydraulic gradient and the corresponding average velocity is listed in Table 1.
Table 1 The hydraulic gradient and the corresponding average velocity in a single fracture
|
Hydraulic gradient |
0.0026 |
0.0020 |
0.0010 |
0.0005 |
0.0016 |
0.0026 |
0.0006 |
|
Velocity of flow(cm/s) |
1.223 |
0.935 |
0.6161 |
0.3895 |
0.7921 |
1.163 |
0.4561 |
|
Hydraulic gradient |
0.0020 |
0.0030 |
0.0046 |
0.0011 |
0.0031 |
0.0055 |
0.0084 |
|
Velocity of flow(cm/s) |
0.902 |
1.353 |
1.812 |
0.6785 |
1.3675 |
2.0363 |
2.696 |
According to Darcy law, ![]() , we
get an equation for calculating the hydraulic conductivity of a single fracture
by fitting the two sets of data. The equation is as follows:
, we
get an equation for calculating the hydraulic conductivity of a single fracture
by fitting the two sets of data. The equation is as follows:
![]() (1)
(1)
The relativity coefficient is 0.79103, and its fitted curve is as follows (In Figure 2):
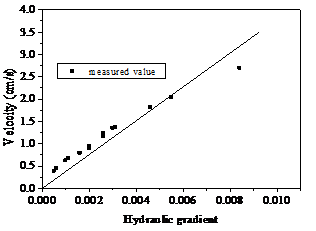
Fig. 2 Hydraulic gradient VS average velocity fitted by Darcy law
From Figure 2 we know: under the condition of this experiment, the flow departs from the Darcy law, and appears non-linear characteristics. The phenomenon can also be observed intuitionally by injecting dye into the fracture. Figure 3 shows the pictures of fracture flow formed when the velocities of flow are 0.935 cm/s and 1.223 cm/s. From Figure 3 we can clearly see that the fracture flow is turbulent flow with such velocity. In this case, it is improper to describe the flow by using the Darcy’s law. As the Darcy’s law is summed up through experiment in the case of one dimension laminar flow of single-phase uncompressible liquid. Therefore, we should consider using non-linear movement equation to analyze the movement equation of fracture water under such hydraulic condition.

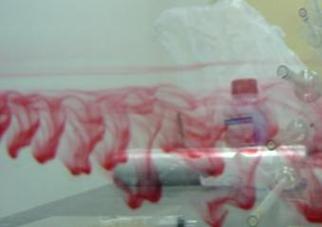
Fig. 3 Flow topographical map (left: 0.935cm/s, right: 1.223cm/s)
3.2 Non-linear movement of single fracture water
The movement of liquid in fracture obeys the non-Darcy law. Here the relation of hydraulic gradient and velocity is non-linear, and it can be showed as:
![]() (2)
(2)
where: a and b are constants decided by experiments. m (1<m≤2) is an index reflecting seepage form.
According to equation (2), we optimize the parameters a, b and m by least square method, and get an equation as:
![]() (3)
(3)
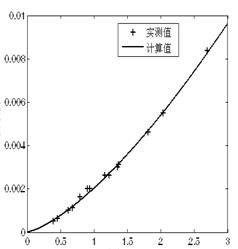
The fitted precision is 1.5348×10-7, and the relativity coefficient is 0.991929. So the fitted precision of this equation is rather good. With equation (3), we can calculate the velocity value of flow. Figure 3.shows the fitted curve of calculated velocity and the measured velocity.
By comparing Figure 2 with Figure 3, we can find that the precision of the fitted experiment data is higher when we use non-linear seepage equation than when we use the Darcy law
+ Measured value Calculated value![]()
![]()
Velocity
(cm/s)
Fig. 3 Hydraulic gradient VS average velocity fitted by nonlinear flow equation
3.3 Reynolds number of the liquid’s flow
The type of liquid’s flow can be judged by the Reynolds number. The formula is:
![]() (4)
(4)
where v is average velocity, d
is hydraulic radius and ![]() is
kinematic viscosity(here we take the value 0.00898 cm2/s
which is under 25OC) With the formula, we can calculate Reynolds
number of different fracture widths and different velocities for analyzing flow
type (Figure 4).
is
kinematic viscosity(here we take the value 0.00898 cm2/s
which is under 25OC) With the formula, we can calculate Reynolds
number of different fracture widths and different velocities for analyzing flow
type (Figure 4).
From Figure 4
we can see: it is obvious that Reynolds number increases as velocity of flow
increases. Another effect factor is hydraulic radium of fracture water. As
hydraulic radium of fracture,width of fracture and water level are relevant,
fracture width’s change with same flux has double-effect to velocity of flow in
fracture and hydraulic radium. According to this we know that the value of
Reynolds number decreases as fracture width increases when other conditions
hold the line.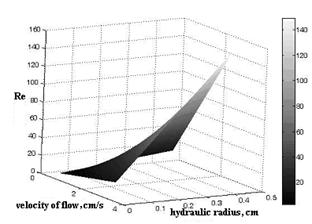
Fig. 4 Relation of Reynolds number, average velocity and hydraulic radium
In addition, we get the minimal value of Re 14.9259, the maximal value 59.9502. The fracture flow appears non-linear seepage phenomenon when Re exceeds14.9259. This value is far less than the critical value of Re 600 of the groundwater movement in slippery single fracture (Lomize(1951)) which means flow form is laminar flow when Re is less than or equal to 600 and the critical value of Re 2300 of the rough single fracture flow(Louis(1969)) which means flow form is laminar flow when Re is less than or equal to 2300. Therefore, the critical value of Re should less than 14.9259 under the experiment condition.
3 Main conclusions
By analyzing the hydraulic data of the experiment, we investigate the characteristics of flow form with different average velocity of flow, analyze the change of flow form and its connection with velocity of flow and provide the Reynolds number of liquid’s non-linear movement. The conclusions are drawn as follows:
(1)Under the experiment condition, the movement of liquid appears non-Darcy flow, and the model for J and v can be written:
![]()
(2)According to the equation of non-Darcy movement, we gain the movement equation of liquid of non-Darcy flow by optimizing parameters. The fitted curve with the measured value is rather good which means the precision of the equation is rather good.
(3)The Reynolds number calculated in the experiment should less than 14.9259. It is far different with the value given by previous studies. The value of Reynolds number increases as fracture flow’s hydraulic radium increases. Fracture width’s change with same flux has double-effect to velocity of flow in fracture and hydraulic radium. The effect is still under study.
Acknowledgements
The research was supported by the National Natural
Science Foundation of
References
[1] Berkowitz, B.,Georg Kosakowski, Gennady, et al. Application of continuous time random walk theory to tracer experiment measurements in fractured and heterogeneous porous media[J]. Ground Water, 2001, 39(4):593-603
[2] Bear, J.
Dynamic of fluids in porous media[M]. New York:
[3] Long, J.C. Porous media equivalents for networks of discontinuous fractures[J]. Water Resources Research, 1982, 18(3): 185-198
[4] Larocque, M., O. Banton, P. Ackerer, and M. Razack. Determining Karst Transmissivities with inverse modeling and an equivalent porous media[J]. Ground Water, 1999, 37(6): 897-903
[5] Dufresne,
D. P., C. W. Drake. Regional groundwater flow model construction and well field
site selection in a karst area,
[6] Field, S. Malcolm. Risk assessment methodology for karst aquifers: (2) solute-transport modeling[J]. Environmental Monitoring and Assessment, 1997, 47(1): 23-37
[7]
Qian Jiazhong, Wang Jiaquan.
Fracture karst water’s modeling and evaluation of water environmental quality
of the north of China[M].Hefei: Press of
[8] Qian Jiazhong, Zhan Hongbin, Zhao Weidong, et al. Experimental study of turbulent unconfined groundwater flow in a single fracture. Journal of Hydrology, 2005, (311):134-142.
[9] Lomize G M. Flow in Fractured Rock (in Russian) [M]. Gosemergoizdat, Moscw, 1951
[10] Romm E S. Flow Characteristics of Fractured Rocks [M]. Nedra,
[11] Su Baoyu, Zhan Meili, Zhao Jian.Study on Fracture Seepage in the Imitative Nature Rock[J].Chinese Journal of Geotechnical Engineering,1995,17(5):19-24
[12] Wang Yuan, Su Baoyu. Research on the behavior of fluid flow in a single fracture and its equivalent hydraulic aperture[J]. Advances in Water Science, 2002,13(1):61-68
[13] Xu Guangxiang, Zhang Yongxing, Ha Qiulin. Super-cubic and sub-cubic law of rough fracture seepage and its experiments study[J]. Shuili Xuebao,2003,(3):74-79
[14] Sun Fenggen, Luo Shaohe, Wang Xinyi. The average equations of fracture flow in a single fracture[J]. Hydrogeology & Engineering Geology, 1996,23(4):25-27
[15] Qian Jia-zhong, Wang Jia-quan, Li Ruzhong, Liu Yong. Formulae for average velocity of groundwater flow and experimental evidence of non-Darcy’s flow through a single fracture[J]. Journal of Hydrodynamics, 2003,Ser. B (6): 56-62




