Evolutional Rules of Regional Groundwater System
The INSTABILITY TREATMENT RESEARCH OF NUMERICAL SIMULATION OF FIELD SOIL WATER
MA Hongyun, LU Wenxi, LI Jun
(Environment And Resource Academic, Jilin
University, ChangChun
Jilin 130026,
Abstract: The simulation period of the field soil water numerical model always lasts for a long period, such as a growth season of crop. On the other hand, the simulation face a problem of inferior stabilization, so we have to use minute volume to difference simulated time in order to make it stable. In allusion to the small rangeability of field soil water in most simulated times, a new method (phase-division-method) was generalized, and it was joined with iteration to lower the instability effect of two main factors (the step-size of time and the representation of water characteristic parameter). By this method, we can use day volume as step-size to run the numerical simulation, and make sure it works under stable and fast. Finally, a section of alfalfa growth season was taken as the investigated subject to test the model we established and the method we generalized. It was confirmed that the method is highly efficient.
Keywords: field soil water, numerical simulation, stabilization, iteration, phase-division-method
Introduction
The stabilization of numerical simulation is about error that may gradually increase in the process of simulating. And if the error becomes too large to make the result valuable, the simulation model will be recognized as instability under some given situation.
Soil water numerical simulation faced a problem of inferior stabilization, because there are a lots of factors work on instability and make the simulating complicated[1]. The factors of instability can be generalized into four main aspects: 1. Soil water simulation equation. Different simulation equation have different stability, but most soil water model that we used today are based on Richards Continuity Equation; 2. Model solution. It included analytical method and numerical method. The result that
calculated by analytical method is precise and without instable problem, but it can only solve some simple questions. We generally solve practical questions by numerical method, which will cause error fated. Finite Difference which belongs to numerical method will be used in this paper; 3. Step-size of discretization. In any numerical simulation, step-size of time and space will directly affect the stability, accuracy and calculating rate. Step-size choice is to find equilibrium in them three. 4. Representation of parameters. The parameters (hydraulic conductivity and diffusivity) are variables which are functions of soil moisture in soil water simulation. A proper algorithm that used to calculate parameters can made it approach its real value better, so that the simulation stability will be insured.
Field soil water numerical simulation lasts for a relatively long period, generally it investigated at least a growth season of crop (120d to 180d) or more. However step-size of time is being restricted into minutes or seconds in order to make the simulating stable, because the simulation model has an inferior stabilization. That is to say simulation time will be divided into ten thousands phases or more, the simulation will last for a long time. To solve this problem, the authors introduce Phase-Division-Method, and integrate it with iteration algorithm. Then we can take 1day as step-size of time and make sure the accuracy of simulating results.
1 Numerical Simulation Model of Field Soil Water
In field, soil water mainly moved along vertical. In this paper, we build vertical one dimension soil water numerical model by continuity equation (A.Richads,1931), boundary and initial conditions.
1.1 Vertical one dimension soil water numerical model
We set soil surface as zero point and vertical downwards as positive axis to build one dimension coordinate system. The model can be expressed as following:
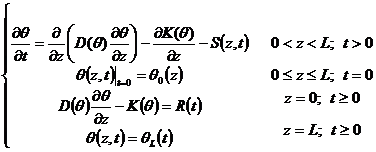 (1)
(1)
Where ![]() is the volumetric water content (mm3/mm3);
is the volumetric water content (mm3/mm3);![]() is the
concentration-dependent soil water diffusivity (mm2/d);
is the
concentration-dependent soil water diffusivity (mm2/d);![]() is the
concentration-dependent hydraulic conductivity (mm/d);z is depth below the soil surface (mm);t is time (d);
is the
concentration-dependent hydraulic conductivity (mm/d);z is depth below the soil surface (mm);t is time (d);![]() is soil water uptake (d-1);L is the total depth (mm);
is soil water uptake (d-1);L is the total depth (mm);![]() is
evaporation intensity and precipitation infiltration intensity (evaporation is negative item and precipitation is
positive item)(mm/d)。
is
evaporation intensity and precipitation infiltration intensity (evaporation is negative item and precipitation is
positive item)(mm/d)。
1.2 The difference of the continuity equation
The differenced implicit expression of one dimension soil water continuity equation is as following [2]:
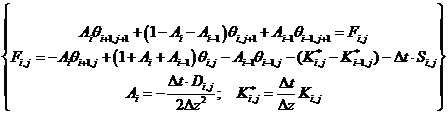 (2)
(2)
Where the subscripts i refer to soil depths and j
refer to times;![]() is
step-size of depth;
is
step-size of depth;![]() is
step-size of time.
is
step-size of time.
1.3 The boundary treatment of the model
The boundary condition generally is part into three types. We are familiar with the first two type of them in soil water simulation, that is the first boundary type (water content of boundary is known) and the second boundary type (water flux of boundary is known).
For the first boundary type, we assume ![]() in equation (2),(i=0
refer to above boundary;i=n+1
refer to nether boundary). Where n
is depth discretized number;
in equation (2),(i=0
refer to above boundary;i=n+1
refer to nether boundary). Where n
is depth discretized number; ![]() is boundary water content.
is boundary water content.
For the second boundary type, we add ![]() into
into ![]() (above boundary) or
(above boundary) or ![]() (nether boundary) of equation
(2). Where the sign of R is decided
by flux direction, if water moves downwards, the sign of R is positive, otherwise negative.
(nether boundary) of equation
(2). Where the sign of R is decided
by flux direction, if water moves downwards, the sign of R is positive, otherwise negative.
1.4 Soil water uptake equation
Soil water uptake is the function of time, depth and water content. It can be expressed by the following experiential equation:
![]()
Where ![]() is soil water uptake validity
equation (which shows how soil water content effects soil water uptake);
is soil water uptake validity
equation (which shows how soil water content effects soil water uptake);![]() is root density distribution equation;
is root density distribution equation; ![]() is transpiration
of crop under fully irrigated.[3]
is transpiration
of crop under fully irrigated.[3]
2 Factor Analysis and Treatment of Instability
To make sure that the simulating is stable, the factors that may cause instability are generalized into four items: a. step-size of time; b. the representation of discrete water content; c. the representation of parameters; d. step-size of depth.
In this four factors, step-size of depth sometimes is confine by test situation and accuracy of simulation. It can not be modulated freely. So we just suggest to making it bigger to benefit the stability of simulation if the accuracy is satisfactory. The representation of discrete water content will cause instability but trifling if it contrasts with effect of the representation of parameters, because the former is 1/50 to 1/1000 times smaller then the latter in quantitatively, the former effect is in the error band of the latter. So the main factors that produce errors are the representation of parameters and step-size of time.
At the following, iteration algorithm was used to eliminate the effect of parameters’ representation, and phase-division-method was used to dispel the effect that cause by time step-size.
2.1 Iteration algorithm be used to eliminate the effect of parameters’ representation
For the parameters is a function of water content,
it is determined by the function expression (experiential equation) and
soil water content. In the process of finite difference,
originally continuous independent variable (water content) was discretized, the
parameters be discretized at the same time. It is the point where the problem
comes from, the problem is each moment of the whole phase time has different
water content value. Then which water content value would be used to calculate
the parameters, so that those parameters may approach the practical value
better Is it the water content value of initial moment or of end moment or other moments The practices proved that
the representation of parameters which be calculated by both water content of
initial moment and end moment are inferior. So iteration algorithm is used to
find the water content of right moment that can represent ![]() of the whole phase. Finally, the
most representative water content is
request to meet equation (5) or (6).
of the whole phase. Finally, the
most representative water content is
request to meet equation (5) or (6).
Hydraulic conductivity and diffusivity are calculated by Brooks-Corey model [4]:
![]() (3)
(3)
![]() (4)
(4)
Where ![]() is the most representative water
content of phase i,
is the most representative water
content of phase i, ![]() is the moisture potential (mm),the subscript s
is the value of saturated,b is constant defined by Brooks-Corey model.
is the moisture potential (mm),the subscript s
is the value of saturated,b is constant defined by Brooks-Corey model.
Then to find more representative parameters is to
find fitted![]() . The following equation is
commonly be used to calculate more representative water content.
. The following equation is
commonly be used to calculate more representative water content.
![]() (5)
(5)
![]() (6)
(6)
Where ![]() is the water content of initial moment
of j time phase;
is the water content of initial moment
of j time phase;![]() is
water content of end moment of j time
phase.
is
water content of end moment of j time
phase.
Process of iteration algorithm is: 1) assume ![]() as water content value of initial
moment; 2) calculate parameters by equation (3) and (4); 3) calculate water
content of the end moment; 4) calculate
as water content value of initial
moment; 2) calculate parameters by equation (3) and (4); 3) calculate water
content of the end moment; 4) calculate ![]() by equation (5); 5) iterate step 2 and
3; 6) evaluating error percentage of water content that calculated out last two
times, if error percentage is unsatisfied then iterate step 4 and 5, otherwise
finish calculation of this phase.
by equation (5); 5) iterate step 2 and
3; 6) evaluating error percentage of water content that calculated out last two
times, if error percentage is unsatisfied then iterate step 4 and 5, otherwise
finish calculation of this phase.
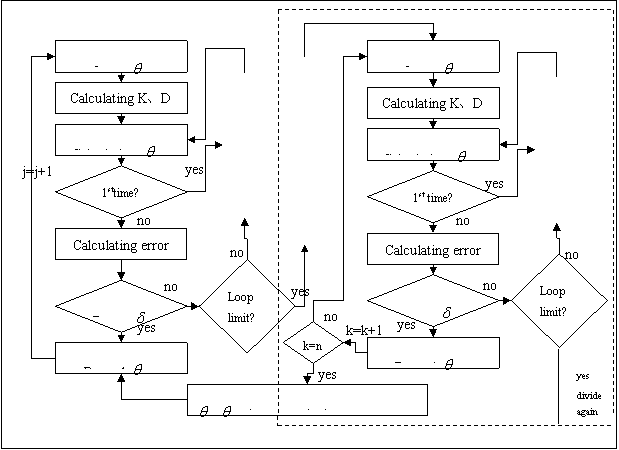
The flow of iteration algorithm is showed in fig.2, out of the broken line frame.
2.2 Phase-division-method was used to dispel the effect of time step-size
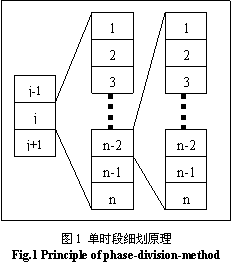 In field soil water numerical simulating, the
rangeability of soil water content is very small except when precipitation or
irrigation happened. Day volume as
step-size to run the numerical simulation would be possible in most of phases.
In some unstable phases, the error percentage may be too large to astringe. To
solve this problem, phase-division-method was generalized, that is we divided a
single phase whose error percentage is too large to astringe into n smaller phases to enhance its
simulating stability. If the error percentage is still too large, we divided it
once more until it gets convergence (see fig.1). We knew it from principium of
numerical method that if only we discrete time tiny enough, we can always make
the model simulated convergent by finite difference method.
In field soil water numerical simulating, the
rangeability of soil water content is very small except when precipitation or
irrigation happened. Day volume as
step-size to run the numerical simulation would be possible in most of phases.
In some unstable phases, the error percentage may be too large to astringe. To
solve this problem, phase-division-method was generalized, that is we divided a
single phase whose error percentage is too large to astringe into n smaller phases to enhance its
simulating stability. If the error percentage is still too large, we divided it
once more until it gets convergence (see fig.1). We knew it from principium of
numerical method that if only we discrete time tiny enough, we can always make
the model simulated convergent by finite difference method.
2.3 Combination of iteration algorithm with phase-division-method
Iteration algorithm and phase-division-method are aimed at different factors to avoid instability. The combination of them two will be more efficient.
Iteration algorithm is familiar to us in numerical simulation, but if error is not being made by inefficient representation of parameters, iteration will get unsatisfied result or go into endless loop. A loop limit was set to solve this problem. When iteration reaches loop limit, this phase will be judged as instable phase, and phase-division-method cut-in to divide the phase into more tiny phases. Fig.2 shows simulation flow of linking iteration algorithm with phase-division-method.
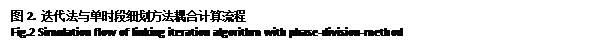
3 Simulation example
A section of alfalfa growth season was taken as the investigated subject to test the model we established and the method we generalized. Soil depth was assumed as 1m, step-size of depth set as 10cm; step-size of time set as 1day; initial total water content set as 325mm; crop root density introduced from reference [5]; simulation period set as 29th June to 20th August; irrigated 35mm and 32mm at 24th July and 12th August respectively.
When a phase is divided by phase-division-method, it was set to divide it into 10 equal length phases; a phase can be divided 5 times worst, that is a phase can small like 10-5day if it need to be.
Simulation result see fig.3 and 4.
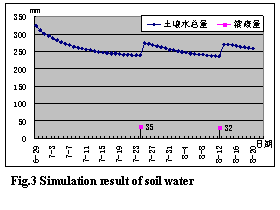 | 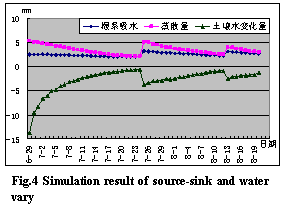 |
Fig.3 shows total soil water content that changes with time and irrigation situation; Fig.4 shows soil water uptake, evapotranspiration (ET) and soil water variational quantity of different times. ET include soil water uptake and evaporation, and soil water variational quantity include ET, groundwater recharge and irrigation quantity.
The figures show that soil water uptake increased after irrigation, but smaller than ET; and then ET gradually approach soil water uptake. That is evaporation reaches its top after irrigation, and then gradually reduces. The nether boundary is drainage before 6th July, for total soil water content is relatively big, presented in fig.4 as soil water variational quantity is bigger than ET in absolute value. After 6th July, the nether boundary become supply boundary, fig.4 shows that soil water variational quantity is smaller than ET in absolute value.
Simulating phases only be divided for one times at 6.29, 7.24 and 8.12 respectively in the whole simulation processes. That is to say, the program finished 54days simulation by divided it into 81 phases. If we take 2 minutes as time step-size, phases will be 38880. The instability treatment we used is very efficient.
Reference:
[1] LEI Zhi-dong, HU He-ping, YANG Shi-xiu. 1999, A review of soil water research. Advances in water science. 10(3):311-318.
[2] Nunzio Romano, Bruno Brunone, Alessandro Santini.,1998. Numerical analysis of one-dimensional unsaturated flow in layered soils. Advances in water resources. 21:315-324.
[3] Lai,C.-T.,Katul,G.,2000.The dynamic role of root-water uptake in coupling potential to actual transpiration. Advances in water resources.23:427-439.
[4]




