Achievements
ANALYTICAL STUDY FOR TIDAL WAVE PROPAGATION IN A COASTAL LEAKY CONFINED AQUIFER SYSTEM:EFFECT OF THE SUBMARINE SILT-INTERFACE
Yuqiang Xia1, Hailong Li1,
2, Qiaona Guo1, Guohui Li1
1 School of
Environmental Studies & (MOE) Biogeology and Environmental Geology Lab,
China University of Geosciences, Wuhan 430074, P. R. China
2 Dept. of Civil and Env. Enggr, Temple University, 1947
N. 12th Street, Philadelphia, PA 19122
Abstract: The structure of a
coastal aquifer system is generally multi-layered, the confined aquifer usually
extends under the sea for a certain distance, and its subcrop is usually
covered by a silt layer. Based on these scenarios, this paper considers a leaky
aquifer system consisting of an unconfined aquifer, a confined aquifer, and a
semi-permeable layer between them. The unconfined aquifer terminates at the
coastline, and the aquifer and the semi-permeable layer (aquifer’s roof) extend
under the sea for a certain distance. The confined aquifer’s subcrop is covered
by a silt layer. The mathematical model for the system is given. The analytical
solution to the model is derived. Our solution extends the existing solutions
obtained by previous researchers. Detailed analyses are conducted to
investigate the influences of aquifer’s extending length, the
semipermeable layer’s leakage, the silt-layer’s dimensionless leakance and loading
efficiency on tidal propagation in the confined aquifer, with focus on the
impacts of leakage through the semipermeable layer, and that of the
silt-layer-subcrop on tidal propagation. The existence of the silt layer
subcrop may significantly decrease the amplitude and increase the phase shift
of the head fluctuation in inland aquifer if the roof length is small. On
the other hand, if the roof length is long enough, the impacts of the silt
layer on the head fluctuation in inland aquifer becomes negligible. The
leakage through the semipermeable layer plays the same role as found by Li and
Jiao [2001, Water Resources Research, 27(5), p1165-1171].
Keywords: Coastal
multi-layered aquifer system, Aquifer extending under the sea, Silt layer,
Analytical solution Tidal wave propagation, Leaky boundary
condition, Leakage
1 Introduction
The coastal area is
where the global economy most developed, and also the most complicated zone for
the earth environmental dynamical system. The groundwater
problems, which have a close connection with the coastal area, for
example, seawater intrusion and land subsidence, become the focal point, which
people pay close attention to gradually. Thereupon, land-ocean interaction in
the coastal zone (LOICZ) has become an active research area in the whole world
nowadays [Yang, 2004]. A great deal of previous studies show that
the research of the tidal propagation in the coastal aquifer system plays an
important and active role in solving various coastal hydrogeological,
engineering geology, ecological and environmental problems related to tidal
dynamics [e.g., Ferris, 1951; Akpofure et al., 1984; Farrell,
1994; Svitil, 1996].
The existing
researches show that the structure of a coastal aquifer system is generally
multi-layered [Van der Kamp, 1973; Jiao and Tang, 1999; Li
and Jiao, 2001a; b; Li and Jiao, 2002; Jeng et al., 2002]. Groundwater head
in inland aquifer will fluctuate with the sea tide, that is, groundwater is
provided with tidal effect. Tidal effect of groundwater in different distance
from the coast is diversified with various aquiferconstructions [e.g., Jacob,
1950; Van der Kamp, 1972; Li and Jiao, 2001a]. Confined
aquifers may exhibit strong tidal effect with fluctuations potentially
extending to several kilometers from coast. Significant fluctuations are
unlikely to extend to more than several decameters from coast in unconfined
aquifers [e.g., White Roberts, 1994; Chen and Jiao, 1999].
The treatment of the aquifer’s boundary condition
directly affects the emulation degree of the aquifer system model in the
research of the coastal aquifer system [Cheng et al.,
2003; 2004]. Most existing studies regard coastline as the boundary of the whole
aquifer system [e.g., Jacob, 1950; Ferris, 1951; Jiao and Tang, 1999]. The depth of
these models built by previous researchers is not less than several
decameters or a hectometer, even much deeper. In reality, however, submarine
relief is a flat gradient sloping down to sea instead of an upheaval in coastal
area [Cheng et al., 2004; Yang, 2004]. The confined aquifer may extend under
the sea with a considerable distance from the coastline [e.g., Li and Chen, 1991a;
b; Li and Jiao, 2001a], even can be deemed them to be an infinite
extendibility in some sea area [Van der Kamp, 1972].
Furthermore,
submarine bank slope lies below the intertidal zone suffered from the effects
of waves and ocean currents. With increase of the depth of seawater, owing to
the weakness of hydrodynamic force and the diminution of sedimentary particles,
silt, clay, and organic oddments may gradually deposit on the seabed, and form
a sedimentary band with interbedded silt, clay, and slit deposit, as well as a
sandwave zone, that is, exogenous sedimentary band [e.g., Yang, 1986;
Zeng et al., 1992]. There is always coastal silt with fuscous and abundant
organic material in an anoxia of the environment. Therefore, the subcrop of
confined aquifer extending under the sea may be indirectly connected to the
seawater, but covered by a thin silt layer; this phenomenon is quite common in
muddy coast [e.g., Li and Chen, 1991b; Yang, 2004]. Li et al. [2006](in press) presented the
analytical solution for a single aquifer in response to the tidal fluctuation
with a thin silt layer boundary, and discussed the influences of the roof
length and hydraulic permeability of the silt layer on the groundwater head
fluctuation.
In this paper,
based on Li and Jiao [2001a] and Li et al. [2006], the authors
consider a more common coastal aquifer system, which has three layers: an
unconfined aquifer, a confined aquifer, and a semi-permeable layer between
them. The confined aquifer extends for a certain distance under the sea, and
its subcrop is covered by a thin silt layer with permeability different from
that of the main aquifer. Considering leaky boundary condition for the
silt layer, the leakage of the semi-permeable layer, and the extending
distance of the aquifer under the sea, a new analytical solution will be
derived. Compared with the existing solutions [e.g., Li and Jiao, 2001a;
Li et al., 2006], an attempt is made to discuss quantitatively the
impacts of the roof length, the semipermeable layer’s leakage, the
silt-layer’s dimensionless leakance and loading efficiency on
tidal propagation in the coastal confined aquifer.
2Model setup and
Analytical Solution
2.1 Conceptual mModel and mathematical
model
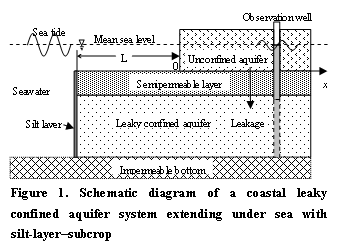
A coastal aquifer
system consisting of an unconfined aquifer, a leaky confined aquifer, and a
semipermeable layer between them is considered in this paper. Assume that the
unconfined aquifer vertically terminates at the coastal line, while the
confined aquifer and the semipermeable layer (roof) extend under the sea
for a certain distance 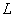 , the bottom of
the leaky confined aquifer is impermeable, all the layers extend landward
infinitely. Let the
, the bottom of
the leaky confined aquifer is impermeable, all the layers extend landward
infinitely. Let the 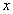 axis be
perpendicular to the coastline, the intersection of the mean sea surface and
the beach face be the origin of the axis, and be positive landward (Figure 1). Based on
the assumption introduced byJiao and Tang [1999], we assume that the
aquifer is horizontal, homogeneous and of constant thickness, and the flow in
the confined aquifer is essentially horizontal and there is
vertical leakage through the semipermeable layer (roof of the confined
aquifer), and the elastic storage of the semipermeable layer is
negligible. Further assume that the density difference between the groundwater
and the seawater can be neglected, owing to density’s slight impact on
groundwater level fluctuation [Hantush and Jacob, 1955; Jiao and Tang, 1999;
Li and Chen, 1991a].
axis be
perpendicular to the coastline, the intersection of the mean sea surface and
the beach face be the origin of the axis, and be positive landward (Figure 1). Based on
the assumption introduced byJiao and Tang [1999], we assume that the
aquifer is horizontal, homogeneous and of constant thickness, and the flow in
the confined aquifer is essentially horizontal and there is
vertical leakage through the semipermeable layer (roof of the confined
aquifer), and the elastic storage of the semipermeable layer is
negligible. Further assume that the density difference between the groundwater
and the seawater can be neglected, owing to density’s slight impact on
groundwater level fluctuation [Hantush and Jacob, 1955; Jiao and Tang, 1999;
Li and Chen, 1991a].
Under above
assumptions and the theories of leaky and elastic aquifers proposed by Hantush and Jacob
[1955] and Jacob [1950], consider the
silt-layer-subcrop, the following mathematical model is derived on
the basis of Li and Jiao [2001a].
The tidal
propagation in the offshore confined aquifer:
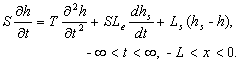 (1)
(1)
The tidal
propagation in inland confined aquifer:
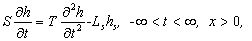 (2)
(2)
(3)
Where 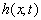 , and denote hydraulic
head [L], storativity (dimensionless),
, and denote hydraulic
head [L], storativity (dimensionless),  and
and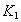 transmissivity [L2T-1]
of the aquifer, respectively;
transmissivity [L2T-1]
of the aquifer, respectively; 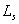 is leakance
or specific leakage [T-1] of the semipermeable layer, which is defined
as
is leakance
or specific leakage [T-1] of the semipermeable layer, which is defined
as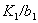 , and are the
thickness [L] and vertical hydraulic conductivity [LT-1] of the
semipermeable layer, respectively;
, and are the
thickness [L] and vertical hydraulic conductivity [LT-1] of the
semipermeable layer, respectively; 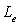 is loading
efficiency (dimensionless), defined as
is loading
efficiency (dimensionless), defined as
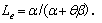 (4)
(4)
where 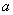 is the
compressibility [M-1LT2] of the confined aquifer
skeleton,
is the
compressibility [M-1LT2] of the confined aquifer
skeleton, 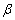 is the
compressibility [M-1LT2] of porosity water in the
confined aquifer, and
is the
compressibility [M-1LT2] of porosity water in the
confined aquifer, and  is the
porosity (dimensionless) of the aquifer;
is the
porosity (dimensionless) of the aquifer; 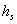 are
hydraulic head [L] of the sea tide,
are
hydraulic head [L] of the sea tide, 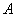 is the
amplitude [L] of the sea tidal, ω is angular
velocity [T-1] of tide and equals
is the
amplitude [L] of the sea tidal, ω is angular
velocity [T-1] of tide and equals 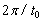 ,
, 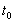 is the tidal
period [T] [Fetter, 1994; Todd, 1980].
is the tidal
period [T] [Fetter, 1994; Todd, 1980].
The pure hydraulic
replenishment is zero at far inland as approaches
infinity,
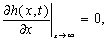 (5)
(5)
and at the coastal
line, i.e., at 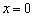 , by the
continuity of hydraulic head and the continuity of flux, respectively, one has
, by the
continuity of hydraulic head and the continuity of flux, respectively, one has
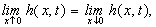 (6)
(6)
 (7)
(7)
Li et al. [2006] presented leaky
boundary condition of silt layer (see equation (8b) of Li et al.), it can be
rewritten as
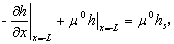 (8)
(8)
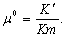 (9)
(9)
The parameter 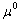 involved in
equation (9) is defined as the relative permeability [L-1] of
the silt layer which describes the leakage of the silt layer relative to the
permeability of the confined aquifer.
involved in
equation (9) is defined as the relative permeability [L-1] of
the silt layer which describes the leakage of the silt layer relative to the
permeability of the confined aquifer.
2.2 Analytical
solution
For convenience of
discussion, two new parameters, the confined aquifer’s tidal propagation
parameter a [L-1] and the dimensionless leakage , are introduced:
are introduced:
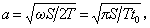 (10)
(10)
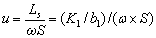 (11)
(11)
The solutions (see Appendix for the
derivation) for the boundary value problem (equations (1)-(8)) are derived as
follows
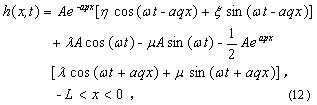
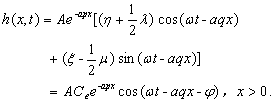 (13)
(13)
where
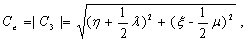 (14)
(14)
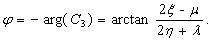 (15)
(15)
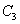 is presented
by equations (A14) and (A16) in the Appendix,
is presented
by equations (A14) and (A16) in the Appendix, 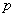 and
and 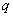 are
determined by the dimensionless leakage
are
determined by the dimensionless leakage  and defined
as
and defined
as
 (16)
(16)
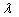 and
and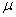 are
controlled by the loading efficiency
are
controlled by the loading efficiency 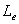 and the
dimensionless leakage
and the
dimensionless leakage , as follows:
, as follows:
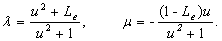 (17)
(17)
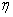 and
and 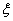 are two
dimensionless constant, defined as
are two
dimensionless constant, defined as
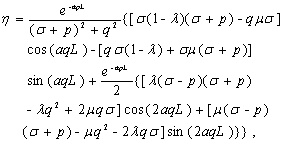 (18)
(18)
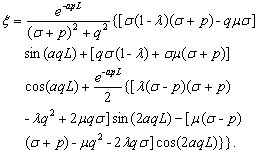 (19)
(19)
where 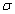 is the
dimensionless leakance of the silt layer, it can be written as
is the
dimensionless leakance of the silt layer, it can be written as
 (20)
(20)
Equations (12) and
(13) are the analytical solution for the tidal propagation in offshore and
inland portion of the confined aquifer, respectively, 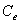 is
comprehensive tidal efficiency of the leaky confined aquifer system,
is
comprehensive tidal efficiency of the leaky confined aquifer system, 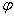 is the
fixed phase shift (radian) and unattached variables x and t.
In addition, Equation (13) shows that the groundwater head fluctuation of an
observation bore at a fixed inland location
is the
fixed phase shift (radian) and unattached variables x and t.
In addition, Equation (13) shows that the groundwater head fluctuation of an
observation bore at a fixed inland location 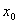 is also
sinusoidal. It can be determined by the groundwater head fluctuation amplitude
is also
sinusoidal. It can be determined by the groundwater head fluctuation amplitude 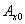 [L] and the time
lag
[L] and the time
lag  [T] of
groundwater response to tidal fluctuation, i.e.,
[T] of
groundwater response to tidal fluctuation, i.e.,
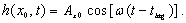 (21)
(21)
Compared with
equation (13), yields
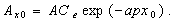 (22)
(22)
 (23)
(23)
The detailed
discussions for  and
and 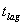 are
presented in section 4.
are
presented in section 4.
3 Compared with Relative Analytical
Solution
Just as
above-mentioned, 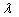 and
and 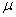 depend upon loading
efficiency
depend upon loading
efficiency 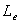 and
dimensionless leakance
and
dimensionless leakance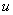 , marked
with
, marked
with 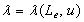 and
and 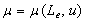 , respectively.
, respectively. 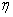 and
and 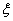 defined by
equations (18) and (19) are determined by four independent parameters, that is,
defined by
equations (18) and (19) are determined by four independent parameters, that is,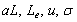 , labeled with
, labeled with  and
and 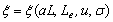 , respectively.
And moreover, the tidal propagations indicated in equations (12) and
(13) are controlled by these parameters, a simple functional relation can
be used to denote the tidal propagations in inland and offshore parts of the
aquifer, viz.
, respectively.
And moreover, the tidal propagations indicated in equations (12) and
(13) are controlled by these parameters, a simple functional relation can
be used to denote the tidal propagations in inland and offshore parts of the
aquifer, viz.
 (24)
(24)
The comparisons
between with existing analytical solutions are given infra, because people
focus all their attention on the tidal propagation in the inland confined
aquifer rather than that of in the offshore confined aquifer, so the authors
only show the expression of the tidal propagation in the offshore aquifer but
no discussion for it because of space limitation.
3.1 Confined Aquifer Extending under the
Sea Infinitely
If the extending
length is magnified infinitely (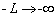 ), i.e.,
), i.e., 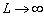 , in view of (18)
and (19), one obtains
, in view of (18)
and (19), one obtains  , then (12) and
(13) can be written as
, then (12) and
(13) can be written as
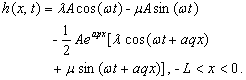 (25a)
(25a)
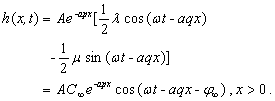 (25b)
(25b)
where
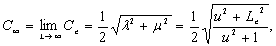 (25c)
(25c)
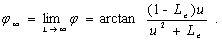 (25d)
(25d)
This solution given
here is the same as the solution obtained by Li and Jiao [2001a] (equations
(21a)-(21c) in Li and Jiao), where the silt-interface is
negligible, which implies that the silt-interface of the confined aquifer
extending under the sea is inexistent when 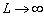 . Here the tidal
propagation is only decided by three parameters, i.e.,
. Here the tidal
propagation is only decided by three parameters, i.e.,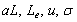 , the functional
relation defined as equation (24) can be written as
, the functional
relation defined as equation (24) can be written as 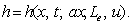 (25e)
(25e)
In this case, if
there is no leakage through the semipermeable layer, viz.,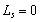 , or
, or 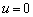 , and from (17),
(16) and (14) one has
, and from (17),
(16) and (14) one has 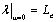 ,
, 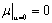 ,
, 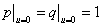 ,
, 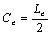 , then
, then
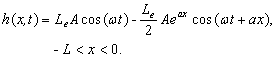 (26a)
(26a)
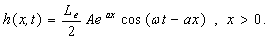 (26b)
(26b)
which is the same
as the result derived by Van der Kamp [1972]. This suggests
the tidal propagation is determined by the loading efficiency 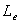 and
and 

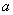 tidal
propagation parameter , that is
tidal
propagation parameter , that is
 (26c)
(26c)
3.2 Confined aquifer without extending
length under the sea
If the offshore confined aquifer extending
length is zero, i.e., 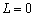 , (18) and
(19) follows that
, (18) and
(19) follows that
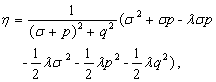 (27a)
(27a)
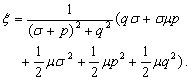 (27b)
(27b)
in view of
equations (14) and (15), yields
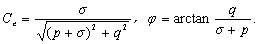 (27c)
(27c)
then the tidal
propagation in confined aquifer can be written as
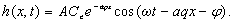 (27d)
(27d)
which is the same
as the solution given by equations (7), (8e), and (8f) in Ren et al.
[2006](in press). In this case, the tidal propagation rest with
three parameters: the confined aquifer’s tidal propagation parameter 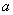 , semipermeable
layer’s leakance
, semipermeable
layer’s leakance  and the silt
layer’s dimensionless leakance
and the silt
layer’s dimensionless leakance 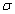 , that is
, that is
 (27e)
(27e)
In this case, if
there is no leakage (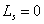 ), viz.,
), viz., 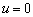 , one has
, one has 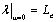 ,
, 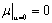 ,
,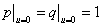 , then yields
, then yields
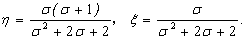 (28a)
(28a)
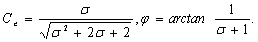 (28b)
(28b)
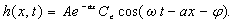 (28c)
(28c)
which accord with
the equations (11) and (12) of Li et al. [2006]. This solution
reflects predominantly that the tidal propagation of confined aquifer 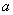 is affected by tidal propagation parameter and the silt
layer’s dimensionless leakance
is affected by tidal propagation parameter and the silt
layer’s dimensionless leakance 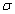 , viz.,
, viz.,
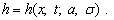 (28d)
(28d)
3.3 Offshore confined aquifer without
silt-interface layer
Assume that there
is no silt layer, the confined aquifer exposes directly itself to the sea,
i.e., the thickness of silt layer  , which is
equivalent to
, which is
equivalent to  in view of
equation (20); or presume that silt layer’s permeability and other
hydrogeologic parameters are not different from that of the confined aquifer,
one can regard silt layer as a part of the confined aquifer, that is,
in view of
equation (20); or presume that silt layer’s permeability and other
hydrogeologic parameters are not different from that of the confined aquifer,
one can regard silt layer as a part of the confined aquifer, that is, 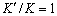 is used in
equation (20). Generally speaking, it is reasonable to assume that the
thickness of the silt layer approximately has an order of magnitude of O(1)
m. On the basis of the nine sets of aquifer parameters obtained by Jiao and Tang
[2001] from various pumping tests in real leaky confined aquifer
systems, the typical ranges of
is used in
equation (20). Generally speaking, it is reasonable to assume that the
thickness of the silt layer approximately has an order of magnitude of O(1)
m. On the basis of the nine sets of aquifer parameters obtained by Jiao and Tang
[2001] from various pumping tests in real leaky confined aquifer
systems, the typical ranges of 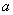 is estimated
to be
is estimated
to be 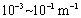 m-1, in
view of (20), the range of
m-1, in
view of (20), the range of 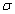 is
is  , it is not
unreasonable to regard
, it is not
unreasonable to regard 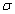 infinity for
thisrange, because its magnitude is much greater than that of other
parameters (
infinity for
thisrange, because its magnitude is much greater than that of other
parameters (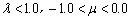 ) in view of (18)
and (19), and follows that
) in view of (18)
and (19), and follows that
 (29a)
(29a)
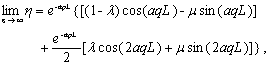 (29b)
(29b)
The solution
obtained under this term is essentially the same as equations (12)-(15),
and equations (29a) and (29b) derived here is uniform with equations (7c)
and (7h) presented in Li and Jiao [2001a].
If there is no
leakage through the semipermeable layer, i.e. 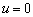 , then
, then  ,
, 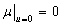 ,
, 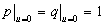 ,
, 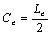 , equations (29a)
and (29b) can be written as follows
, equations (29a)
and (29b) can be written as follows
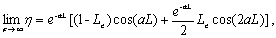 (30a)
(30a)
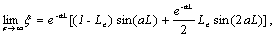 (30b)
(30b)
According to
equations (14) and (15), one yields
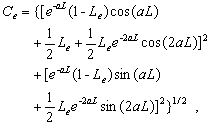 (30c)
(30c)
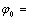
 (30d)
(30d)
the tidal
propagation in confined aquifer can be written as
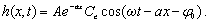 (30e)
(30e)
which agrees with
equations (16a), (16b) and (16c) derived by Li and Jiao [2001a]. And the
groundwater head is impacted by tidal propagation parameter 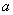 , the
dimensionless extending length
, the
dimensionless extending length  , loading
efficiency
, loading
efficiency
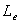 , and the silt
layer’s dimensionless leakance
, and the silt
layer’s dimensionless leakance 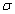 , it is follows
that
, it is follows
that
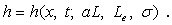 (30f)
(30f)
Under this
condition, if there is no extending length, that is,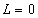 , (29a) and (29b)
can be simplified as follows:
, (29a) and (29b)
can be simplified as follows:
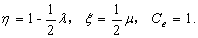 (31a)
(31a)
 (31b)
(31b)
This solution is
exactly the same as the analytical solution introduced by Jacob [1950].
3.4 Offshore confined aquifer with an
impermeable silt-interface layer
If the hydraulic permeability
of the thin silt layer is quite weak, i.e., the dimensionless leakance =0.0, one obtains
 (32a)
(32a)
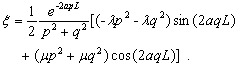 (32b)
(32b)
the form of
solution obtained under this condition is the same as equations (12)-(15) in
this paper.
Further assume
that there is no replenishment for confined aquifer, viz., the leakage through
the semipermeable layer is zero, that is , 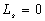 or
or 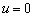 , then
, then 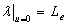 ,
, 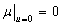 ,
, 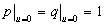 , one can yield
, one can yield
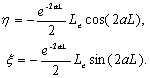 (33a)
(33a)
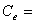
 (33b)
(33b)
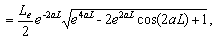
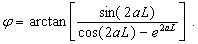 (33c)
(33c)
the tidal
propagation in confined aquifer can be presented as
 (33d)
(33d)
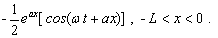 (33e)
(33e)
which is exactly
the same as equations (13a) and (13b) obtained by Li et al. [2006]. The tidal
propagation is enslaved to tidal propagation parameter 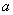 , the
dimensionless extending length
, the
dimensionless extending length  , and loading
efficiency
, and loading
efficiency 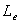 , viz.,
, viz.,
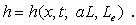 (33f)
(33f)
If there is no
extending length under this condition, that is, , equations (18)
and (19) can be simplified to
, equations (18)
and (19) can be simplified to
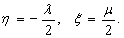 (34)
(34)
According to these
assumptions, it is obvious to yield 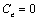 , that is,
, that is, 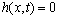 , which indicates
that the confined aquifer is enclosed with an impermeable silt layer, so the
groundwater head is not tampered withtidal propagation, and is a constant,
which is anastomotic with actual fact.
, which indicates
that the confined aquifer is enclosed with an impermeable silt layer, so the
groundwater head is not tampered withtidal propagation, and is a constant,
which is anastomotic with actual fact.
4 Influences of Various Parameters on Tidal
Propagation
On the basis of
the nine sets of aquifer parameters obtained from various pumping tests in real
leaky confined aquifer systems by Jiao and Tang
[2001], the typical ranges of 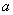 and
and  are
estimated to be
are
estimated to be 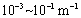 and
and 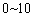 , respectively [Li and Jiao, 2001a]. For this study,
a larger range of
, respectively [Li and Jiao, 2001a]. For this study,
a larger range of 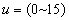 is used, the
sea tide is assumed to be diurnal with a period
is used, the
sea tide is assumed to be diurnal with a period 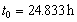 , and the
dimensionless distance of the piezometer at the inland area is
, and the
dimensionless distance of the piezometer at the inland area is 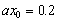 from the
coastline. An attempt is made to discuss the impacts of dimensionless
roof length
from the
coastline. An attempt is made to discuss the impacts of dimensionless
roof length  , the
semipermeable layer’s dimensionless leakage
, the
semipermeable layer’s dimensionless leakage  , the
silt-layer’s dimensionless leakance
, the
silt-layer’s dimensionless leakance 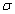 , and loading
efficiency
, and loading
efficiency 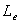 on tidal
propagation in confined aquifer.
on tidal
propagation in confined aquifer.
4.1 Influences of dimensionless roof length and leakage through the
semipermeable layer
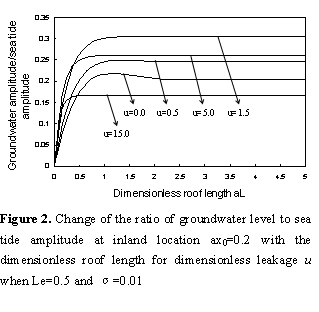
As show in Figure 2, for any
dimensionless leakage , when the
silt-layer’s dimensionless leakance 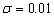 and
and 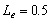 , the amplitude is
quite small, even equals zero at inland area
, the amplitude is
quite small, even equals zero at inland area 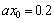 when
when 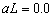 . This is
because the silt-layer can be regarded as impermeable layer, that is,
there is no tidal propagation in the coastal confined aquifer under this
condition. But the amplitude is raised significantly as the dimensionless roof
length
. This is
because the silt-layer can be regarded as impermeable layer, that is,
there is no tidal propagation in the coastal confined aquifer under this
condition. But the amplitude is raised significantly as the dimensionless roof
length  increases
when it is small. For the curve of
increases
when it is small. For the curve of 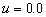 , the increase
of the amplitude is induced by the loading efficiency
, the increase
of the amplitude is induced by the loading efficiency 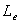 which acts
on the offshore confined aquifer, and the amplitude approaches a constant and
is no longer sensitive to the roof length when the dimensionless roof length is
greater than a certain value.
which acts
on the offshore confined aquifer, and the amplitude approaches a constant and
is no longer sensitive to the roof length when the dimensionless roof length is
greater than a certain value.
Figure 2 also shows that the amplitude increases
as  is increased
from 0 to 1.5, but it decreases as
is increased
from 0 to 1.5, but it decreases as  is increased
further from 1.5 to 15.0. This is because the leakage from the inland
portion tends to damp the tidal propagation in the confined aquifer,
while the leakage from the offshore part will enhance the tidal
propagation. When the dimensionless leakage is small and the roof length is
great, the enhancing effect due to the offshore leakage is dominant; Li and Jiao [2001a] have presented the
detailed explanations.
is increased
further from 1.5 to 15.0. This is because the leakage from the inland
portion tends to damp the tidal propagation in the confined aquifer,
while the leakage from the offshore part will enhance the tidal
propagation. When the dimensionless leakage is small and the roof length is
great, the enhancing effect due to the offshore leakage is dominant; Li and Jiao [2001a] have presented the
detailed explanations.
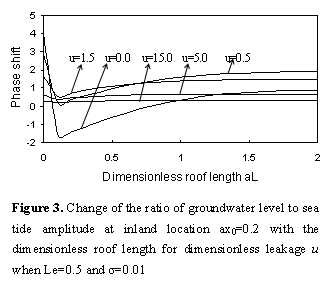
Based on
above-mentioned assumptions, it is easy to see that the influence of
dimensionless leakage  on phase
shift is non-monotonic in Figure 3. The phase shift
changes from a large positive value to a large negative value when
on phase
shift is non-monotonic in Figure 3. The phase shift
changes from a large positive value to a large negative value when  equals zero
and the dimensionless roof length is very small. Then the phase shift increases
with
equals zero
and the dimensionless roof length is very small. Then the phase shift increases
with  , and is no longer
sensitive to the roof length when
, and is no longer
sensitive to the roof length when  reaches a
certain value.
reaches a
certain value.
When  is larger
than 0.5, there is only positive phase shift occurring. The change of phase
shift is non-monotonic for the curve
is larger
than 0.5, there is only positive phase shift occurring. The change of phase
shift is non-monotonic for the curve  of in Figure 3. When
of in Figure 3. When is small, the phase
shift reduces significantly begin, and then increases slowly. While there is a
minute decrease or no change when is great,
which shown in Figure 3 with two curves
is small, the phase
shift reduces significantly begin, and then increases slowly. While there is a
minute decrease or no change when is great,
which shown in Figure 3 with two curves 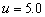 and
and 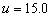 . When the
dimensionless roof length is greater than a certain value, these curves tend to
different positive values. Figure 3 also shows
that the phase shift increases with
. When the
dimensionless roof length is greater than a certain value, these curves tend to
different positive values. Figure 3 also shows
that the phase shift increases with  when
when  increases
and
increases
and  is small. On
the contrary, the phase shift decreases with
is small. On
the contrary, the phase shift decreases with  when
when  increases
and
increases
and  is large.
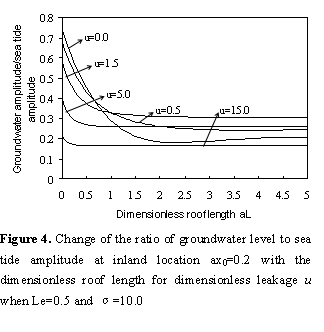
is large.
For 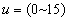 , at inland area
, at inland area 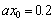 when the
silt-layer’s dimensionless leakance
when the
silt-layer’s dimensionless leakance 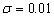 and
and 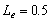 , as shown in Figure 4, the amplitude
decreases with the dimensionless roof length
, as shown in Figure 4, the amplitude
decreases with the dimensionless roof length  when
when  is small.
This is because the tidal propagation in the confined aquifer is mostly damped
when the dimensionless roof length
is small.
This is because the tidal propagation in the confined aquifer is mostly damped
when the dimensionless roof length  increases.
But when
increases.
But when  reaches a
certain value, the amplitude tends to a constant. This accords with the
discussion in section 3.3 of Li and Jiao [2001a]: there is a
threshold value for roof length, and when the roof length is greater than
threshold value, the water level fluctuation will behave as if the roof length
were infinite.
reaches a
certain value, the amplitude tends to a constant. This accords with the
discussion in section 3.3 of Li and Jiao [2001a]: there is a
threshold value for roof length, and when the roof length is greater than
threshold value, the water level fluctuation will behave as if the roof length
were infinite.
In addition, if the
silt-layer’s dimensionless leakance 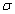 is very
large, it is equivalent to the permeability of silt layer is same as the
confined aquifer, one can regard that there is no silt layer as discussed in section
3.3. The effect of the dimensionless leakage
is very
large, it is equivalent to the permeability of silt layer is same as the
confined aquifer, one can regard that there is no silt layer as discussed in section
3.3. The effect of the dimensionless leakage  on the
amplitude is same as the Figure 2 in Li and Jiao [2001a].
on the
amplitude is same as the Figure 2 in Li and Jiao [2001a].
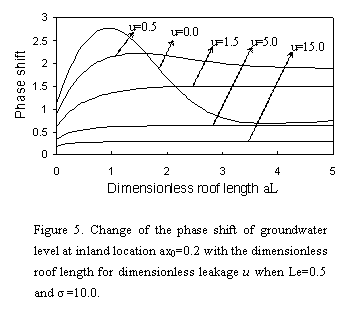
The phase shift is
positive value at inland area 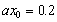 when
when  and
and 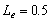 , as shown in Figure 5, for the curve
, as shown in Figure 5, for the curve 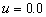 , the change
of phase shift is complex. To begin with, there is a rapid increase, and then is
a slow decrease. Once there is leakage through semipermeable layer, the
change of phase shift is monotone increasing with
, the change
of phase shift is complex. To begin with, there is a rapid increase, and then is
a slow decrease. Once there is leakage through semipermeable layer, the
change of phase shift is monotone increasing with  . And there is no
variation for phase shift when
. And there is no
variation for phase shift when  is large
enough. In addition, the phase shift decreases as
is large
enough. In addition, the phase shift decreases as  increases.
increases.
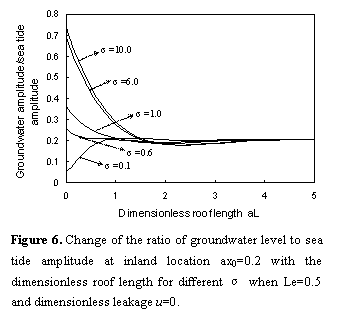
4.2 Influence of silt-layer’s dimensionless leakance
At inland area 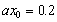 , forany
dimensionless leakance
, forany
dimensionless leakance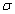

 , assume
, assume 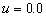 and
and 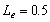 , as shown in Figure 6, the amplitude
increases significantly with the dimensionless roof length
, as shown in Figure 6, the amplitude
increases significantly with the dimensionless roof length  when
when  is small and
is small and 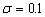 . But the
amplitude decreases significantly when
. But the
amplitude decreases significantly when 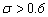 . And when
the dimensionless roof length is greater than a certain value, the
amplitude is a constant. Figure 6 also shows that the amplitude increases
as
. And when
the dimensionless roof length is greater than a certain value, the
amplitude is a constant. Figure 6 also shows that the amplitude increases
as 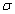 increases.
It is close to the permeability of the confined aquifer when the
silt-layer’s dimensionless leakance
increases.
It is close to the permeability of the confined aquifer when the
silt-layer’s dimensionless leakance 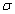 is very
large, and the damping effect of the silt layer may be small, which is of
great benefit to the tidal propagation in confined aquifer.
is very
large, and the damping effect of the silt layer may be small, which is of
great benefit to the tidal propagation in confined aquifer.
According to
above-mentioned assumptions, Figure 7 shows that
the curves of phase shift are non-monotonic functions. When 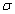 equals zero and
equals zero and  is terribly
small, the phase shift falls rapidly from 3.87 to -1.56, after that, it
increases quickly with
is terribly
small, the phase shift falls rapidly from 3.87 to -1.56, after that, it
increases quickly with  and then
slowly. When the dimensionless roof length is greater than a certain value,
these curves tend to a positive value. Phase shift only appears positive values
when
and then
slowly. When the dimensionless roof length is greater than a certain value,
these curves tend to a positive value. Phase shift only appears positive values
when 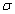 is lager
than 0.4. As shown in Figure 7with the curve
is lager
than 0.4. As shown in Figure 7with the curve  , phase shift
decreases significantly begin and then laggardly when
, phase shift
decreases significantly begin and then laggardly when  is small.
When
is small.
When 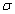 is large, as
shown in Figure 7 with the curves
is large, as
shown in Figure 7 with the curves 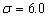 and
and  , the phase shift
increases significantly begin and then decreases laggardly. Finally, these
curves reach a positive value.
, the phase shift
increases significantly begin and then decreases laggardly. Finally, these
curves reach a positive value.
The general trend
shown in Figure 7 is: when both dimensionless roof length  and
dimensionless leakance
and
dimensionless leakance 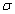 are small ,
phase shift decreases significantly begin and then rises laggardly to a
constant. However, for a large
are small ,
phase shift decreases significantly begin and then rises laggardly to a
constant. However, for a large 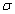 , phase shift rises
significantly begin and then decreases laggardly to a constant. Figure 7 also shows
that the initial phase shift decreases as
, phase shift rises
significantly begin and then decreases laggardly to a constant. Figure 7 also shows
that the initial phase shift decreases as 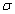 increases;
this also suggests that the increase of the silt-layer’s
dimensionless leakance is benefit for tidal propagation in confined
aquifer.
increases;
this also suggests that the increase of the silt-layer’s
dimensionless leakance is benefit for tidal propagation in confined
aquifer.
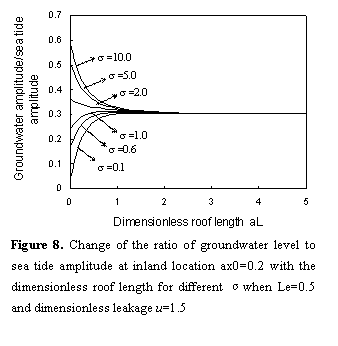
If there is a large leakage through, assume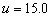 and
and 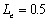 , for any
dimensionless leakance
, for any
dimensionless leakance 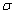 , at inland area
, at inland area  , Figure 8 shows that
theamplitude raises rapidly with
, Figure 8 shows that
theamplitude raises rapidly with  when it is
small as
when it is
small as  changes from
0.1 to 1.0. But the amplitude decreases significantly when
changes from
0.1 to 1.0. But the amplitude decreases significantly when 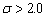 under the
same assumptions. As shown in Figure 7, Figure 8 also shows
that the initial phase shift decreases as
under the
same assumptions. As shown in Figure 7, Figure 8 also shows
that the initial phase shift decreases as 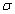 increases,
this suggests that the increase of the silt-layer’s dimensionless leakance
is benefit for tidal propagation. Compared Figure 6 with Figure 8, it is obvious
that the semipermeable layer’s leakage will damp the enhancing effect of the
silt-layer’s dimensionless leakance
increases,
this suggests that the increase of the silt-layer’s dimensionless leakance
is benefit for tidal propagation. Compared Figure 6 with Figure 8, it is obvious
that the semipermeable layer’s leakage will damp the enhancing effect of the
silt-layer’s dimensionless leakance 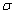 on tidal
propagation, this result has been pointed out in section 4.1.
on tidal
propagation, this result has been pointed out in section 4.1.
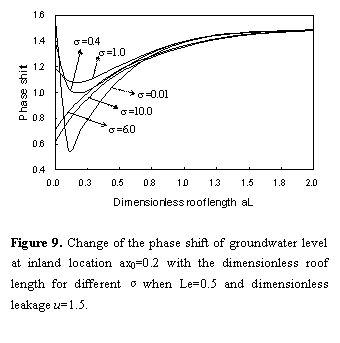
The phase shift is
positive value as shown in Figure 9 when we use
the same conditions considered in Figure 8. When dimensionless
roof length  is small and
dimensionless leakance
is small and
dimensionless leakance 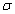 is very small
is very small 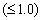 , the phase shift decreases
significantly begin and then rises laggardly to a constant. But when a large
, the phase shift decreases
significantly begin and then rises laggardly to a constant. But when a large 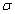 is used, phase
shift rises significantly begin and then rises laggardly to a constant. Figure 9 also shows
that the initial phase shift decreases with
is used, phase
shift rises significantly begin and then rises laggardly to a constant. Figure 9 also shows
that the initial phase shift decreases with 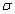 ; this
suggests that the increase of the silt-layer’s dimensionless leakance
is benefit for tidal propagation again.
; this
suggests that the increase of the silt-layer’s dimensionless leakance
is benefit for tidal propagation again.
If Figure 7 was compared
with Figure 9, one can see that the phase shift changes with a
positive range in Figure 9. The two figures indicate that the
initial phase shift and amplitude variation of tide waves are decreased
significantly, under the comprehensive action of the semipermeable layer’s
leakage andthe silt-layer’s dimensionless leakance.

4.3 Influence of loading efficiency
The loading
efficiency reflects the groundwater level fluctuation caused by compression of
both the aquifer skeleton and groundwater, due to the loading rate of seawater
above the roof of the confining layer. Solution obtained by previous
researchers shows that the impact of the loading efficiency on fluctuation is
significant only when the leakage of the semipermeable layer is small
and the roof length is great [Li and Jiao, 2001a]. According to
section 4.2, one can easily receive the information that the influence of the silt-layer’s
dimensionless leakance  on tidal
propagation is small when
on tidal
propagation is small when 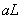 is very
large; on the other hand, when
is very
large; on the other hand, when 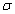 is enough
large, this condition is similar to the case that there is no
silt-layer-subcrop considered by predecessor. In view of these results, we
discuss the effect of the loading efficiency on fluctuation only when
is enough
large, this condition is similar to the case that there is no
silt-layer-subcrop considered by predecessor. In view of these results, we
discuss the effect of the loading efficiency on fluctuation only when  , dimensionless
leakage
, dimensionless
leakage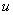 , and
, and 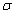 are very
small,
are very
small, ,
, 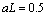 ,
, 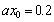 are used in
lower section.
are used in
lower section.
When 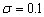 , compared three
curves
, compared three
curves 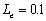 ,
, 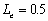 , and
, and 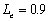 in Figure 10, the
amplitude is largest and the phase shift is smallest when
in Figure 10, the
amplitude is largest and the phase shift is smallest when 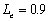 , and per contra
for curves with
, and per contra
for curves with  and
and  . That is, the
amplitude oscillation and the time lag of the groundwater head fluctuation
responses to sea tide increases and decreases with loading efficiency,
respectively.
. That is, the
amplitude oscillation and the time lag of the groundwater head fluctuation
responses to sea tide increases and decreases with loading efficiency,
respectively.
Contrasted 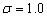 with
with 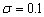 when we keep
the same assumptions used in Figure 10, as shown in Figure 11, three curves
when we keep
the same assumptions used in Figure 10, as shown in Figure 11, three curves ,
, 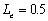 , and
, and 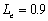 are close to
each other. Just as above-mentioned, the increase of the silt-layer’s
dimensionless leakance is favorable for tidal propagation. It is seen
intuitively that the amplitude oscillation for
are close to
each other. Just as above-mentioned, the increase of the silt-layer’s
dimensionless leakance is favorable for tidal propagation. It is seen
intuitively that the amplitude oscillation for 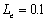 changes from
0.05 to 0.13 as
changes from
0.05 to 0.13 as 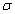 is increased
from 0.1 to 1.0. Corresponsively, the amplitudes for
is increased
from 0.1 to 1.0. Corresponsively, the amplitudes for  and
and 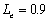 change from 0.18
and 0.30 to 0.22 and 0.32, respectively, which also incarnate the rule that the
amplitude oscillation and the time lag of the groundwater levels response to
sea tide increases and decreases with loading efficiency, respectively.
change from 0.18
and 0.30 to 0.22 and 0.32, respectively, which also incarnate the rule that the
amplitude oscillation and the time lag of the groundwater levels response to
sea tide increases and decreases with loading efficiency, respectively.


5. Conclusions
The structure of a
coastal aquifer system is generally multi-layered, and the confined aquifer
usually extends for a certain distance under the sea. This has been
observed and studied analytically and numerically by many previous researchers. An analytical
solution is derived in this paper to investigate the tidal propagation in a
coastal leaky confined aquifer with a thin silt-layer-interface. Several
solutions obtained by previous researchers are obtained when give some certain
values to roof length 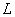 , the
semipermeable layer’s leakage
, the
semipermeable layer’s leakage 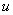 , and the
silt-layer’s dimensionless leakance
, and the
silt-layer’s dimensionless leakance 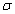 ,this shows that
analytical solution presented here is more general than the traditional
solution presented by previous researchers. And the detailed discussions for
the influences of thedimensionless roof extending length, the
semipermeable layer’s leakage, the silt-layer’s dimensionless leakance, and loading
efficiency on the amplitude and the phase shift of the groundwater head
fluctuation in inland confined aquifer were analyzed. The analyses show that
the effects of the leakage from the inland and offshore portions of the
semipermeable layer are different. The leakage from the inland portion tends to
damp the water level fluctuation in the confined aquifer, while the leakage
from the offshore part will enhance the fluctuation. When the dimensionless
leakage is small and the roof length is great, the enhancing effect due to the
offshore leakage is dominant. The amplitude oscillation increases with loading
efficiency, butthe time lag of the groundwater head fluctuations response to
sea tide decreases. Owing to the existence of the silt layer subcrop,
which is equivalent to a certain extension for the roof length of the confined
aquifer, the amplitude oscillation and the phase shift of the tidal waves are
held down and increased, respectively. And the increase of the
silt-layer’s dimensionless leakance is favorable for tidal propagation, but
the leakage of the semipermeable layer will damp this promoter action, it
always makes phase shift positive, and no negative phase shift occurs. Compared
with the condition that there is no leakage through the semipermeable layer,
the initial phase shift and amplitude variation of tide waves is decreased
significantly under the comprehensive action of the semipermeable layer’s
leakage and the silt-layer’s dimensionless leakance.
,this shows that
analytical solution presented here is more general than the traditional
solution presented by previous researchers. And the detailed discussions for
the influences of thedimensionless roof extending length, the
semipermeable layer’s leakage, the silt-layer’s dimensionless leakance, and loading
efficiency on the amplitude and the phase shift of the groundwater head
fluctuation in inland confined aquifer were analyzed. The analyses show that
the effects of the leakage from the inland and offshore portions of the
semipermeable layer are different. The leakage from the inland portion tends to
damp the water level fluctuation in the confined aquifer, while the leakage
from the offshore part will enhance the fluctuation. When the dimensionless
leakage is small and the roof length is great, the enhancing effect due to the
offshore leakage is dominant. The amplitude oscillation increases with loading
efficiency, butthe time lag of the groundwater head fluctuations response to
sea tide decreases. Owing to the existence of the silt layer subcrop,
which is equivalent to a certain extension for the roof length of the confined
aquifer, the amplitude oscillation and the phase shift of the tidal waves are
held down and increased, respectively. And the increase of the
silt-layer’s dimensionless leakance is favorable for tidal propagation, but
the leakage of the semipermeable layer will damp this promoter action, it
always makes phase shift positive, and no negative phase shift occurs. Compared
with the condition that there is no leakage through the semipermeable layer,
the initial phase shift and amplitude variation of tide waves is decreased
significantly under the comprehensive action of the semipermeable layer’s
leakage and the silt-layer’s dimensionless leakance.
Appendix: Derivation of the solution to (1)-(8)
Assume 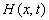 is a complex
function, let
is a complex
function, let  and
and 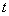 are independent
variables for convenience using separation of variables to solve the equations,
and use
are independent
variables for convenience using separation of variables to solve the equations,
and use 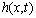 as its real
part, that is
as its real
part, that is
 (A1)
(A1)
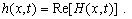 (A2)
(A2)
where 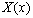 is an
unknown function of
is an
unknown function of 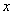 ,
, 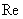 denotes the
real part of the complex expression,
denotes the
real part of the complex expression,  .
.
Based on these
assumptions, substituting (A1) into the equations (1)-(8) which 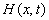 satisfies,
yields
satisfies,
yields
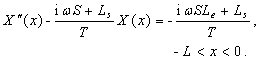 (A3)
(A3)
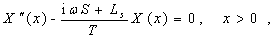 (A4)
(A4)
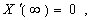 (A5)
(A5)
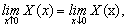 (A6)
(A6)
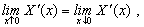 (A7)
(A7)
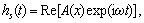 (A8)
(A8)
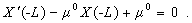 (A9)
(A9)
The general solutions of (A3) and (A4) are followed
 (A10)
(A10)
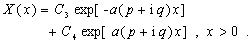 (A11)
(A11)
where 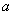 ,
,  and
and 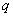 ,
,  and
and 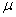 are defined
by (8), (10) and (11), respectively.
are defined
by (8), (10) and (11), respectively. 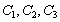 and
and 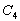 are unknown
complex coefficients. Substituting the boundary condition equations
(4)-(7) into (A10) and (A11), one yields
are unknown
complex coefficients. Substituting the boundary condition equations
(4)-(7) into (A10) and (A11), one yields
 (A12)
(A12)
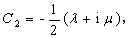 (A13)
(A13)
 (A14)
(A14)
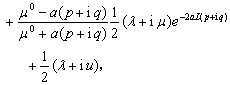
 (A15)
(A15)
make some routine calculations for (A12) and (A14), they can be written as follows
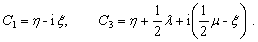 (A16)
(A16)
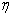 and
and 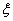 are
constants defined by (18) and (19), respectively. Substituting (A13),
(A15) and (A16) into (A10) and (A11) can obtain the solution of the
are
constants defined by (18) and (19), respectively. Substituting (A13),
(A15) and (A16) into (A10) and (A11) can obtain the solution of the 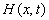 , then substitute into, and acquire the
real part of, finally leads to
the solutions for the boundary value problems (1)-(8) given by (12) and (13).
, then substitute into, and acquire the
real part of, finally leads to
the solutions for the boundary value problems (1)-(8) given by (12) and (13).
Acknowledge
This research is
supported by the National Natural Science Foundation of China (NSFC No.
40372111). The authors are very grateful to Ms. Ying Yang for her much
help.
References
[1] Akpofure, E. T.,
A. L. James, and H. D. C. Alexander. Boundary integral solution to seawater
intrusion into coastal aquifers. Water Resour. Res., 20(8), 1150-1158, 1984.
[2] Chen Chongxi, and Jiao, J. J.. Numerical simulation of pumping tests in multilayer
wells with non-Darcian flow in the wellbore. GroundWater, 37(3), 465-474, 1999.
[3] Cheng Jianmei et
al.. Determination of seaward boundary with three dimensional density dependent
tidal effect model: by example of coastal aquifers in Jiahe River Basin, Shandong Province.
Earth Sci. J. China Univ. Geosci., 28(2), 255-232, 2003.
[4] Cheng Jianmei, Li
Guomin and Chen Chongxi. Numerical study on salt water intrusion into
freshwater aquifer in the coastal zone and island. Wuhan: China University of
Geosciences Publisher, 71-75, 2004.03 (Chinese).
[5] [5] Farrell, E.
R.. Analysis of groundwater flow through leaky marine retaining structures.
Geotechnique, 44(2), 255-263, 1994.
[6] Ferris, J. G..
Cyclic fluctuations of water level as a basis for determining aquifer
transmissibility. International Assoc. of Scientific Hydrology. Publ. 33,
148-155, 1951.
[7] Fetter CW. Applied
hydrogeology. Englewood Cliffs, NJ: Prentice-Hall; 98, 376, 1994.
[8] Hantush, M. S.,
and C. E. Jacob, Non-steady radial flow in an infinite leaky aquifer, Eos
Trans. AGU, 36(1), 95-100, 1955.
[9] Jacob, C. E., Flow
of groundwater, in Engineering Hydraulics. edited by H. Rouse, John Wiley, New
York, 321-386, 1950.
[10] Jeng D. S., L. Li
and D. A. Barry. Analytical solution for tidal propagation in a coupled
semi-confined/phreatic coastal aquifer. Adv. Water Resour., 25(5),
577-584, 2002.
[11] Jiao, J. J., Tang, Z. H.. An analytical solution of groundwater
response to tidal fluctuation in a leaky confined aquifer. Water Resour. Res.,
35(3), 747-751, 1999.
[12] Jiao, J. J., and Tang, Z. H.. Reply to comment by R. E. Volker and Q.Zhang on “An
analytical solution of groundwater response to tidal fluctuation in a leaky
confined aquifer” by J. J. Jiao and Z. Tang. Water Resour. Res., 37(1),
187-188, 2001.
[13] Li, H., and Jiao, J. J.. Tide-induced groundwater fluctuation in a coastal leaky
confined aquifer system extending under the sea. Water Resour. Res., 37(5),
1165-1171, 2001a.
[14] Li, H., and Jiao, J. J.. Analytical studies of groundwater-head fluctuation
in a coastal confined aquifer overlain by a semi-permeable layer with storage.
Adv. Water Res., 24(5), 565-573, 2001b.
[15] Li, H., and Jiao, J. J.. Analytical solutions of tidal groundwater flow in
coastal two-aquifer system. Adv. Water Resour., 25(4), 417-426, 2002.
[16] Li Guomin, and
Chen Chongxi. Determining the length of confined aquifer roof extending under
the sea by the tidal method. J. Hydrol., 123, 97-104, 1991a.
[17] Li Guomin, and
Chen Chongxi. The determination extending under the sea by analysis of
groundwater level fluctuations. Earth Sci. J. China Univ. Geosci., 16(5),
581-589, 1991b.
[18] Svitil, K. A..
Groundwater secrets. Discover, 17(9), 28, 1996.
[19] Todd, D. K..
Groundwater Hydrology. John Wiley, New York, 235-247, 1980.
[20] Van der Kamp, G..
Tidal fluctuations in a confined aquifer extending under the sea. Proc. Int.
Geol. Congr., 24th, 101-106, 1972.
[21] Van der Kamp, G...
Periodic flow of groundwater. Ph.D. dissertation, Free University of Amsterdam.
The Netherlands, 1973.
[22] White, J. K., and
T. O. L. Roberts. The significance of groundwater tidal fluctuations, in
Groundwater Problems in Urban Areas. Edited by W. B. Wilkinson, Inst. of Civ. Eng., London,
31-42, 1994.
[23] Yang Dianying.
Oceanography. Higher Education Press, 343-344, 1986, 5 (Chinese).
[24] Yang Zigeng.
Geological oceanography. Tsinan: Shandong Education Press, 2004, 12
(Chinese).
[25] Zeng
Chengkui et al.. Chinese marine scientific research and development. Qingdao Press,
158, 1992.12 (Chinese)




