Liqun Chen ^1,4, Changming Liu ^1,2, Fanghua Hao ³

(1 Institute of Geographical sciences and Natural Resources Research, CAS, Beijing 100101 China

2 college of water science, Beijing Normal University, Beijing 100875, China

3 School of Environment, Beijing Normal University, Beijing 100875, China

4 Graduate school of Chinese Academy of sciences, Beijing 100039, China)

Abstract: The purpose of this study is to identify and assess the change of baseflow and impacts of climate factors on it in the source regions of the Yellow River, based on analyses of long hydrological time series (1956-2000) from four subbasins of the source regions of the Yellow River and the whole source regions of the Yellow River. Kalinin baseflow separation technique has been improved based on the characteristics of climate and streamflow of the study regions then applied to estimate baseflow. Statistical method is adopted in order to investigate the effect of climate factors on baseflow. Annual mean baseflow in the source regions of the Yellow River is 13.246 billion m³, accounting for more than 60% of the total runoff of the area interested. Annual baseflow is in direct proportion to annual precipitation. The sharp rise in temperature in the 1990s decreased baseflow significantly. The impacts of climate factors on baseflow are different in different subcatchment. In subbasin above Huangheyan hydrologic station which is relative cold and arid with annul mean temperature of -3.84 °C and the water area accounted for 7.95% of the subbasin, both temperature and precipitation nearly had no direct impacts on baseflow on annual time scale. The increasing temperature thaws frozen soil more rapid thus lowers the groundwater table and lake water level, hence decreases water supply of baseflow from groundwater and lake water. In subbasin between Huangheyan and Jimai hydrologic station baseflow are influenced both by precipitation and temperature but the response rate of baseflow to precipitation is more rapid that than temperature. In subbasin between Jimai and Maqu hydrologic stations precipitation and temperature aree two key factors impacting baseflow but the effect of precipitation is more pronounced than temperature, while in subbasin between Maqu and Tangnaihai hydrologic station precipitation is the only climate factor affecting baseflow in short term. The factors inducing serious decrease of baseflow in the 1990s are also investigated into.

Key words: Yellow River, baseflow, precipitation, temperature

The characteristics of many terrestrial ecosystems, for example, are heavily influenced by water availability and, in the case of instream ecosystems and wetlands, by the quantity and quality of water in rivers and aquifers (McCarthy et al., 2001). Consequently, there have been a great many studies on changes in the regional hydrological cycle (Thomas, 2000; Burn and Elnur, 2002) and the potential effects of climate change on hydrology (focusing on cycling of water) and water resources (focusing on human and environmental use of water).Baseflow is an important genetic component of streamflow, which comes from groundwater storage or other delayed sources (shallow subsurface storage, lakes, melting glaciers, etc.) (Smakhtin, 2001). Discharge in most rivers is strongly dominated by outflow from a shallow groundwater reservoir exfiltrating through the banks and the bottom not only in rainless periods but also during rainstorm events. Information on baseflow characteristics provides threshold values for different water-based activities and is required for such water resource management issues as water supply, irrigation, and water quality and quantity estimates.

The Yellow River, originating from the Yueguzonglie basin on the northern part of the Bayankela Mountain in Tibet highlands at el. 4,500 m is flowing through nine provinces, with a total length of 5,464 km, basin area795,000 km² and, finally empties itself into the Bohai sea (Including isolated inflow area 42,000 km²) . It is the second largest river in China, and downstream being protected area of 120,000 km² from flooding. The total population within river basin is 107 million, the cultivated land is 12 million ha. The irrigated areas in the river basin and that downstream along both banks outside the basin reach 7.33 million ha in total. In the 1990s, the runoff of the Yellow River decreased seriously. It’s important to research into the change of water cycle in Yellow river.

The regions above Tangnaihai hydrologic station are the main runoff generation areas which contribute more than 35% of the total runoff with 15.3% of the total area, and are less affected by human activities. In the 1990s runoff of Tangnaihai hydrologic station experienced a serious decrease which had attracted considerable attention(Wang, 2003; Zhang et al., 2004; Liu, 2004). Liu C M(2002) investigated the Changes in components of the hydrological cycle in the Yellow River basin during the second half of the 20th century. Zheng (2003) researched the temporal runoff distribution of the study regions. Wang(2004) based on the geologic and physiognomy conditions investigated the conversion relationships between the river and groundwater in the Yellow River drainage area. However, the above studies did not provide an in-depth analysis on baseflow especially on the source regions of the Yellow River.

This paper tries to detect factors impacting on baseflow in the source regions of the Yellow River basin during the second half of the 

20th century, by applying correlation analysis. The second section deals with data availability and the methodology used. In the next 

section of the paper, a simplified description of the improved Kalinin baseflow separation technique is introduced, and they provide 

the base for further analysis in the following sections. The fourth section presents the results and impacts of climate change baseflow 

are discussed. The paper ends with a short summary.

Study Area and Data Sources

The source regions of the Yellow River referred as the regions above Tangnaihai hydrological station in the Yellow River basin, locates between 95°50’45”E-103°28’9”E and 32° 12’11”-35°48’7”N(Figure 1) with the area of 122217Km². The study area is in the northeast of the Qinghai-Tibet Plateau which is 3000 ~5000m above the sea level and famous as Roof of the World. The elevation ranges from the peak of Alnima of 6282m to the valley of Tongde basin of 2,665m with the fall of 3617m and average of 4000m. A series of mountains on it stretch from the northwest to the southeast, with snow and glacier on the tops all year around. The head-stream area of the Yellow River and its tributaries, the Heihe River, and the Baihe River, are plain district with grassland, lakes and swamps. The channel length is 1553Km and the river slope averages of 1.1‰ within the study area. The rainfall is influenced by the climate of Bengal’s sea and Pacific with maximum average monthly rainfall in summer accounts for 75% to 90% and minimum in winter (Figure 2). Precipitation events were characterized by long duration, low intension and large cover extent. The annual precipitation varies from 250mm to 750mm. The mean annual flow at Tangnaihai hydrologic station is calculated at 649m³/s or 204.70 ×10⁸m³/a more than 35% of that of the Yellow River. There is snowmelt runoff in these regions. Snowmelt runoff is the dominant form of runoff during winter and spring, while runoff from rainfall is dominant form of runoff during summer and fall. The source regions of the Yellow River contribute more than 35% of runoff of the total Yellow River With 15.3% of area thus were named as the “water tower of the Yellow River”. With the change of climate, surfacial and subsurfacial conditions and the development of Chinese economy the runoff of the study area have experienced several times runoff corrupt, and the annual runoff decreased seriously in the 1990s. The study regions are divided into 4 subbasins as control sections at the location of the four hydrologic stations(Huangheyan, Jimai, Maqu, Tangnaihai)(Figure 1).

Due to the low population and economic development level in the area, very few data collection points exist in the basin. Figure 1 present and list the location of the hydrometeorological used herein. The precipitation and temperature of each subbasin are computed using arithmetical mean of the metrological data of the subbasin.

Method

Pearson correlation coefficient

Pearson’s correlation coefficient, which functions as a measure of similarity between variables, measures the strength and direction (decreasing or increasing, depending on the sign) of a linear relationship between two variables X and Y and can be defined as:

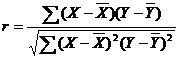(1)

Where and denote the means of the two variable. Let A and B be climate factors and runoff respectively in the sample. The row X denotes the value of the climate, while the row Y denotes the value of the climate. If A and B are relative agreement, then the value of r will be high, whose positive (negative) sign tokens linear increasing (decreasing). A nonparametric method is suggested to estimate the statistical significance of a computed correlation coefficient.

Baseflow separation

Kalinin baseflow separation technique can be interpreted as follows: the base flow is simulated as outflow from a linear reservoir with recession constant ; the streamflow exceeding the outflow from the reservoir is divided between recharge to the groundwater store and direct runoff with a constant partitioning factor. This last assumption is a gross simplification of reality. Kalinin baseflow separation technique proposed by Kalinin (cited by Ding Zhili et al ,2003) is written as:

（1）

Where:

（2）

is the average runoff of time step n-1 and n, is the baseflow of time step n-1, is the recession constant, and is a coefficient determined by trials or errors or by experiences.

Kalinin method was originally applied to whole water year. In the study regions there nearly no direct flow in winter, as showed in figure 2, precipitation is low and temperature is fairly below zero the precipitation is in the form of snow. There nearly no surfaces flow so it is unsuitable to apply equation(1) to separate baseflow in winter. The following in this section will propose improvements to Kalinin method suited for the study regions.

Kalinin baseflow separation technique includes two parameters: recession constant and ratio coefficient β. The recession constant is derived from recession curve during time periods with no or low rain or recharge. Although Wittenberg and Sivapalan(1999) claimed nonlinear relationship between the groundwater discharge and the reservoir storage of shallow unconfined aquifers, T. Chapman found that the linear storage model can still be used as a very good approximation in most cases. The recession curve plots as a straight line in a semilogarithmic plot of t against log Qt and recession constant is the absolute value of the slope coefficient. Recession constant is affected by precipitation, evaporation (Wittenberg and Sivapalan, 1999) and flow data errors. In this research, recession curves in winter are selected and the following two criteria should be satisfied when estimating recession constants:1) the days of the recession curve should exceed 30; 2) the Nash coefficient should be greater than 0.95 when linear regression fit is applied. As in Figure 3 the recession constant is 0.0255.

Ratio coefficient β was determined on trials with the principle that each day the estimated baseflow should be less than streamflow. Theoretically, baseflow should coincide with recession curve in recession periods, but, in practice, as there exists some reading error or others factors affecting recession curve, there are some discrepancies between baseflow and recession curve. Thus according the climate characteristics of the study area, the following steps are proposed to separate baseflow:

Prepare input data one year at a time, including daily flow data, direct flow starting date(rising point as showed in Figure 4) and the recession constant;

Initialize coefficient β with a range. Define an interval to retrieve the coefficient β in the range from the low bound to the high bound. In this paper the coefficient β is initialized to the range of [0.5,4.0] and the interval is 0.01;

During time periods out of recession(namely the time periods from the rising point to flection point, see Figure 4), using ratio coefficient β retrieved in step (2) once at a time, daily flow data, and recession coefficient as input to function (1) to estimate baseflow process. If the estimated baseflow process intersect with streamflow process, discharge the ratio coefficient β, else storage it.

In recession period(the periods after flection point in Figure 4) using the ratio coefficient achieved in step (3) once at a time, daily flow data and recession coefficient as input to function (1) to optimize the final ratio coefficient β. Least square sum: is used as the optimization criteria. Where is the observed streamflow and is the estimated baseflow at time step i in recession periods.

Apply equation (1) to the whole calendar year with daily runoff, the β coefficient derived in step (4), the recession constant and the direct flow begin date-the rising point as showed in Figure 4 to separate baseflow from streamflow.

1)                                 Repeat the steps (1) to (5) to separate baseflow from streamflow of the next year, until the ending year.

These improvements reduced the input parameters and make the baseflow separation process more simple and objective.

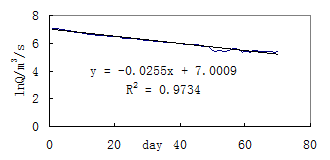
Fig. 3 Computation of recession coefficient of Tangnaihai Hydrologic Station of 1958                                                     

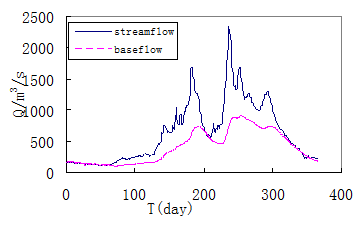
Fig. 4 The runoff component separation of Tangnaihai hydrologic station of of 1958

Results and Discussions

Dynamic variation of the baseflow in the source regions of the Yellow River

Table 2 shows the fundamental hydrologic characteristics of the study area with average annual precipitation of 640.67×10⁸m³, runoff of 203.8×10⁸m³, temperature of -0.52℃ and baseflow of 132.46×10⁸m³. BFI is the abbreviation of Baseflow index means the ratio of annual baseflow to runoff.

Table 1 Baseflow of the source regions of the Yellow River

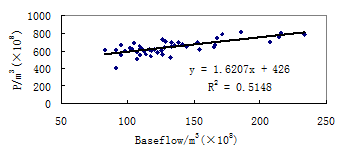
Fig. 5 plots of annual baseflow against annual precipitation in the source regions of the Yellow River

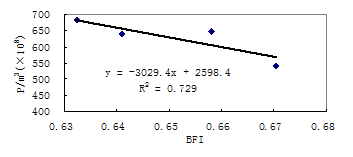
Fig. 6 plots of 10 years averages precipitation against baseflow index of the source regions of the Yellow River

Mean baseflow and precipitation are highest in the 1980s and lowest during time periods of 1956 to 1960 among the time periods listed in table 1.There existed good linear relationship between annual baseflow and precipitation, and with the increase of precipitation baseflow will increase (Figure 5). Points of the plot of mean baseflow index against precipitation of every 10 years shows a strong negative linear relation (Figure 6) while those of the plot of annual mean precipitation against baseflow index are scattered. These facts showed that precipitation had noticeable impacts on baseflow index on 10-year-scale while had nearly no impact on annual time scale. This may due to the increase or decrease trend of precipitation in long term will affect the Surfcial or subsurfcial features to change the runoff generation processes, and so change the relative volume of direct flow and baseflow. Surfcial features include area, shape, channel network, slope, vegetation, roughness and land use. Subsurfcial features are soil texture, structure and type; porosity; stratigraphy; hydraulic conductivity; and geological controls. The study regions locate in the highland, the human activities is relative weak. The rising rate of temperature is 0.51℃/10a in the 1990s which are significant greater than that of other time periods as listed in table 1. Since the human activities and precipitation remains relatively stable we can conclude the decrease of runoff and baseflow in the 1990s can be attributed to the quickly rising of temperature.

Dynamic change of the baseflow of subbasins of the study area

Separate baseflow from streamflow of Tangnaihai, Maqu, Jimai and Huangheyan hydrologic station with daily flow data, then accumulate the daily series to annual series. The baseflow, direct flow and total runoff of each subbasin presented in Figure 1 are computed; correspondingly the precipitation and temperature in each subbasins are calculated from the meteorological station in each subbasin.

Table 2 Baseflow of the Head regions of Yellow River

Head regions of Yellow River are the area above Huangheyan hydrologic station of the Yellow River with area of 20930 Km². The area is really cold and arid with annual average temperature of -3.85 °C and precipitation of 65.524×10⁸m³. The elevation is above 4200m. There were 4077 lakes in 1950s among which 48 lakes was bigger than 0.5 Km², and the total water area were 1664.6Km² which was7.95% of the Head regions.

The average annual runoff is 6.40×10⁸m³, and baseflow of 3.82×10⁸m³ which accounts for more than half of the runoff. The average baseflow index is 0.556. The correlate coefficients of precipitation and temperature against baseflow can’t pass the test of significance at the level of 0.05 using value of annual or even moving average of 5 years. This result shows in this region temperature and precipitation has no or low effect on baseflow in short time period. Zhang Shifeng et al (2004) showed that in this region the actual evaporation is in direct portion to temperature, and the soil water storage is continuous decrease. There were only about 2000 lakes in the 1990s which is half of that in 1950s and water level of the lakes had decreased seriously. The temperature rising rate averaged 0.32/10a(Figure 7) from 1956 to 2000 and 0.40/10 in the 1990s(Table 2). The quickly rising of temperature increased the actual evaporation and accelerates the smelt of frozen soil. With the smelt of frozen soil the groundwater level and lake water level will move downward, and thus may result in the decrease of water supply of baseflow from soil and lakes. So we can easily explain the seriously decrease of baseflow in the 1990s while annual mean precipitation in the 1990s is the biggest.

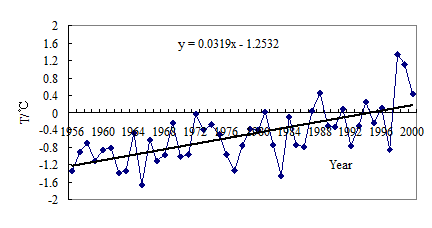
Fig.7 Annual Temperature of Maduo metrological station since 1956

Table 3 baseflow in subbasin between Huangheyan and Jimai hydrologic station

The area of subbasin between Huangheyan and Jimai hydrologic station is 25479Km², with the elevation above 4000m. This subbasin is relative cold and arid with average annual temperature of -3.84°C, annual average precipitation of 95.79 ×10⁸m³. The annual average runoff is 33.61×10⁸m³, baseflow of 19.27×10⁸m³ and baseflow index of 0.588.

Precipitation and baseflow shows a good linearship while points of the plot of baseflow against temperature are relative scattered on annul time scale. The correlation coefficient with moving average of 3 years of temperature against baseflow is -0.523 which could pass the test of significance at the level of 0.01. Thus conclusion could be made that in this region precipitation and temperature both have significant impact on baseflow but the extent and response rate are different: precipitation’s impact is stronger and more quick than that of temperature. Table 3 shows that the temperature rising rate in the 1990s is 0.33℃/10a which is higher than any other time periods listed in table 3. In the 1990s the decrease of precipitation and the increase of temperature contributed largely to the significant decrease of baseflow.

The area of the Subbasin between Jimai and Maqu hydrologic stations is 40580km² and elevation is above 3400m. The pondage ability is noticeable for the well developed river network and large tributaries of Heihe River, Baihe River on the right side of the Yellow River in this region(Figure 1). Heihe River and Baihe River are plain district with grassland, lakes and swamps. This subbasin is characterized by abundant of precipitation with annual average precipitation of 267.371 ×10⁸ m³ and respondingly the annual average runoff is noticeable high of 103.673×10⁸ m³ more than 50% of that of the source regions of the Yellow River; the annual average baseflow is 68.82×10⁸ m³ and the mean baseflow index is 0.649.

Table 4 baseflow in subbasin between Jimai and Maqu hydrologic station

The correlate coefficient of annual precipitation against baseflow is 0.618 which is significant at the level of 0.01. Correlate coefficient of annual temperature against baseflow is -0.353 which could pass the test of significance at the level of 0.05. In this subbasin precipitation and temperature are two important factors influencing baseflow but the impact of precipitation is more pronounced than that of temperature on baseflow.

Figure 8 shows that average precipitation and baseflow index of each ten years has good negative linear relationship. From table 4 we could see baseflow index reach maximum in 1960s and minimum in 1980s and the temperature rising rate before 1990 was 0.2℃/10a while 1.2℃/10a in the 1990s. According to the change of baseflow index we could conclude that in the 1990s the decreasing rate of baseflow was greater than that of direct runoff and the impact of temperature on baseflow is significant than that on direct flow in 10 years time scale in this region.

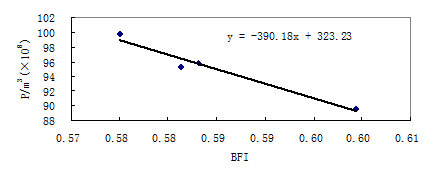
Fig. 8 plots of means of 10 years precipitation against baseflow index of subbasin between Jimai and Maqu hydrologic station

Subbasin between Maqu and Tangnaihai hydrologic stations, with area of 35228Km² and elevation above 2700m, annual average precipitation of 143.099×10⁸ m³, annual average temperature of 0.53°C , annual average runoff of 59.712 ×10⁸ m³ , average baseflow index of 0.704. Runoff, precipitation, experienced a serious decrease in 1990s while temperature and baseflow index are higher than the average (Table 2).

Table 5 baseflow in subbasin between Maqu and Tangnaihai hydrologic station

The correlate coefficient of baseflow against precipitation is 0.616 which are significant at the level of 0.01 while the correlate coefficient of baseflow again precipitation can’t pass the test of significance even with moving average of 5 years which shows in this region the baseflow only influenced by precipitation in short term. Significant decrease of precipitation in the 1990s is a vital factor attributes to the decrease of baseflow.

Summary

Kalinin baseflow separation technique is improved based on the characteristics of the climate and streamflow of the study area and baseflow are separated with daily flow data during time periods of 1956 to 2000. Impacts of temperature and precipitation on baseflow are analyzed. Results shows baseflow accounts for more than half of the runoff in the study area, baseflow index is 0.556 in subbasin above Maduo hydrologic station, 0.588 in area between Huangheyan and Jimai, 0.649 in area between Jimai and Maqu and 0.704 of area between Maqu and Tangnaihai. Precipitation is a vital factor affects the volume of baseflow in the source regions of the Yellow River, and in 1990s the significant increase of temperature plays an important role in the decrease of baseflow. The impact of temperature and precipitation on baseflow are different on different subbasin in the source regions of the Yellow River. In the Head regions of Yellow Rive, both temperature and precipitation have low or no direct impact on baseflow. The increasing temperature thaws the frozen soil which will lower the groundwater table and water level of lakes thus decreased the baseflow. In subbasins between Huangheyan and Maqu hydrologic station both temperature and precipitation are an important factors impact on baseflow. In region between Maqu and Tangnaihai hydrologic station temperature nearly has no impact on baseflow while precipitation shows noticeable impact on baseflow in short term. These results show with the increase of temperature the impact of temperature on baseflow gradually become weak till no direct on it in short term.

While worth be noticed is there are many glaciers, in this paper the influence of glaciers on baseflow are not discussed. With the increase of temperature the snowmelt runoff will increase so the impact of decrease of precipitation or increase of temperature on the baseflow will more strong. And also Because of the sparsely of the meteorological station more efforts should be afford to monitor changes of the precipitation and temperature and subsurfical or surfical condititions.

Acknowledgment

Funding for this study was provided by the Major State Basic Research Development Program of China (Grant No: G19990436-01) and Chinese National Natural Science Foundation(NO.40471127).