1 Introduction

Non-Fickian behaviors, e.g. the scale-dependent dispersion and early breakthrough times, and long time tails in measured breakthrough curves (Berkowitz et al., 2002), are quite often observed for solute transport in soils and natural aquifers due to the heterogeneities of porous media in different scales. Accurate characterization of early arrival time behavior is particularly significant for wiping off contaminants from subsurface waste repositories, and exactly delineation the late time tailing behavior is importance for ground water remediation.

 

 

The hydrodynamic dispersion theory (Bear, 1972) is one of the most commonly used for describing the solute transport in porous media. And the advection-dispersion equation (ADE) deduced from the theory is based on two major assumptions: one is that the center of mass of the solute plume travels with the average fluid velocity, and the other is the dispersion behaves macroscopically as Fikican diffusive process, with the dispersivity being assumed constant in space and time. For one-dimensional flow, the ADE for non-reactive solute is given by:

(1)

where C is the solute concentration, D_d,ij is the hydrodynamic dispersion coefficient, and v_i is the average pore velocity of solute transport, x_i is the distance, and t is the time. The ADE has been found with reasonable accuracy in describing the contaminant migration in aquifers with relatively small degrees of heterogeneity (Garabedian et al., 1991) and in small-scale experiments (Bear, 1972), but as shown in literatures (Levy and Berkowitz, 2003; Cortis and Berkowitz, 2004; Bromly and Hinz, 2004), non-Fickian transport has been observed even in small-scale, relatively homogeneous, laboratory-scale models, and the ADE fails to capture it.

Benson (1998) and Benson et al. (2000a, b) applied the Lévy motion theory to describe the spatial and temporal distribution of solute concentration, and a partial differential equation named the fractional advection-dispersion equation (FADE) was derived based on this theory. Then FADE was used to simulate the non-Fickian transport process for conservative solute (Pachepsky et al., 2000; Huang et al., 2006) and adsorbing solute (Huang and Huang, 2004) respectively. From these researches, FADE is capable of describing the non-Fickian transport to some extent; however, the dispersion coefficient of FADE was found in scale-dependent (Huang et al., 2005; Lu et al., 2002).

The continuous time random walk (CTRW) theory was applied by Berkowitz and Scher (1995, 1997, 1998) to describe the transport in geological media, i.e. porous and fracture media. Berkowitz et al. (2002), Cortis and Berkowitz (2004) developed the general CTRW equation, and three kinds of transition probability density functions, i.e., the asymptotic model (ASY), the truncated power law model (TPL), the fractional-in-time derivative equation (FDE) were proposed to characterize the breakthrough curves (BTCs). Application of CTRW to quantify the laboratory tracer test (Berkowitz et al., 2000; Levy and Berkowitz, 2003; Cortis and Berkowitz, 2004) and the field tracer migration (Berkowitz and Scher, 1998; Kosakowski et al., 2000) indicated that CTRW is a good method to characterize non-Fickian transport both in porous media and fractures medium.

In this paper, we used the general CTRW model in conjunction with the ASY, TPL and FDE to model the solute transport in 1250cm long heterogeneous soil column, and the change pattern of the model parameters was analyzed.

2 Theory

CTRW theory is based on particle migration is represented as a sequence of displacements. The heart of the CTRW formulation is to determine the transition probability density function y(s,t), which describes each particle transition over a distance and direction s in time t.y(s,t) reflects implicitly the influence of properties of porous media, degree of water saturation, fracture matrix and adsorption or desorption. And y(s,t) can be decouple into p(s)y(t), wherey(t) is probability rate for transition time t, and p(s) is probability distribution of jump lengths, and it is assumed to have finite first and second moments. According to the central limit theorem and after a sufficiently large number of steps, the sum of the displacement will be in Gaussian distribution from the outset. Under this uncoupling assumption, anomalous behavior can arise with a power law, transit-time distribution:

(2)

The temporal formulation of the governing probability density function is referred to as the standard CTRW (Margolin and Berkowitz, 2002) in contrast to the Lévy flight formulations or mixed case of wide distributions in both space and time. In analogy to a commonly used derivation of the Fokker-Planck equation from a master equation, Berkowitz et al. (2002) considered a general CTRW model and obtained a Fokker-Planck equation as a particular case. This equation is equivalent to a continuous time random walk over a range of length scales on which the statistical homogeneity can be assumed.

The one-dimensional Fokker-Planck Equation with Memory (FPME) for the Laplace transformed concentration can be described as:

(3)

(4)

(5)

(6)

where is a memory function which accounts for the unknown heterogeneities at the pore scale, t is some characteristic time, and v_y and D_y are the transport velocity and generalized dispersion coefficient, respectively. The variable u is the Laplace variable. The dimensionless dispersivity, a_y=D_y/v_y.

Three types of transition time distribution y(t), i.e., asymptotic form, truncated power law form and fractional-in-time form were proposed and used (Cortis et al., 2004).

(1) Asymptotic y(t)

is the Laplace transform of y(t).

(7)

Cortis et al. (2004) referred to this model as the asymptotic form. This form of y(t) is closely related to the general algebraic form y(t)~t^(-1-β) which has been a foundation of CTRW theory.

(2) Truncated power law y(t)

Dentz (2004) presented the transition time distribution by a truncated power law distribution, y(t) is in the following form

(8)

and the Laplace transform of y(t) is given by

(9)

where t₂=t₂/t₁ and G(a,x) is the incomplete Gamma function. For transition time t₁<<t<<t₂, y(t) behaves according to a power law, y(t)µ(t/t₁)^-1-b. In the time range, the transport behavior is anomalous for 0<β<2. While for t>>t₂, y(t) decreases exponentially, the transport behavior is Fickian. For β>2 the transport becomes Fickian already for t>>t₁ and the upper cutoff t₂ plays only a minor role on the transport behavior. Thus this form emphasizes the intermediate range algebraic behavior and the crossover time to normal transport discussed above (Dentz et al., 2004).

(3) Fractional-in-time derivative equation y(t)

When

(10)

Eq. (3) will reduce to the fractional-in-time derivative equation (Berkowitz et al., 2002).

3 Experiment of Large Heterogeneous Saturated Soil Column

Huang et al. (1995) conducted laboratory experiments of tracer transport in a 12.5 m long, horizontally placed soil column with cross-section areas of 10cm×10cm under steady state saturated flow conditions to investigate the scale effect.

In this experiment one heterogeneous column was packed, which was filled with a wide range of soil materials including clay, fine-, medium-, and coarse textured sands, gravel, and pebbles of 1 to 2cm in diameter, as well as various mixtures of these materials. On average, the particle size decreased gradually from very coarse at the inlet to relatively fine at the outlet. The porosity n was approximately 0.45 for clay and about 0.33 for the other materials. After a steady state flow was established, the NaCl solution as the tracer was injected into the soil column. Electrical conductivity probes were installed laterally 100 cm intervals in the column for measuring the solute concentration during the experiments. The flow rate was 0.192 cm/min for the heterogeneous soil column.

As we have known, this experiment is one of the longest soil columns used for testing scale-dependent transport in laboratory scales. Detailed information of the experiments can be found from Huang et al. (1995).

4 Results and Discussion

The CTRW Matlab Toolbox Version 1 developed by Cortis and Berkowitz (Cortis and Berkowitz, 2005) has been used to fit the BTCs at difference distances from the inlet of the soil column. And a Neumann boundary condition was considered at the outlet. With the measured twelve BTCs for the heterogeneous soil column, we estimated the values of parameters in ADE, ASY, TPL and FDE as shown in Table 1. It can be seen that the dispersion coefficient of ADE increases to 121.39cm²/min at x=800cm which is larger than the value 12.797cm²/min at x=300cm with one order in magnitude. The maximum generalized dispersion coefficient is found at x=700cm with values of 797.58cm²/min, 317.95 cm²/min and 126.790 cm²/min for TPL, ASY and FDE, respectively (see Table 1). The result is due to the non-homogeneous nature of the soil column, especially between x=600cm and 800cm. As discussed by Huang et al. (1995), relatively high values of dispersion coefficient at 700cm appear to be the result of heterogeneities in the form of nearly horizontal lenses. Therefore, solute spreading at 700cm has been enhanced.

For TPL, the lowest β value is 0.912, the highest β value is 1.535, and most β values are larger than 1.0. The general velocity is found in large variation with highest value of 67.15cm/min and lowest value of 1.055cm/min. For ASY, the lowest β value is 0.53 at x=600cm, while at other distances the β values range from 0.86 to 1.1. The general velocity varies in some extent with an average value of 1.5cm/min and a standard deviation of 0.8 cm/min. For FDE, β has a value of 0.920±0.019 and the general velocity value is 1.57±0.3cm/min. Both β and the general velocity are relatively stable. Relatively large variations in both β and the general velocity values of TPL and ASY may partially attribute to the specific forms of TPL and ASY functions. The results suggest that it is possible to describe the non-Fickian transport in such a heterogeneous soil column by using CTRW with a single-β-value’s FDE function and stable velocity value.

As shown in Table 1, the differences between the fits of the general CTRW with TPL, ASY and FDE and experimental data are smaller than those between the fits of ADE and the measured data. And no significant differences are found among the three CTRW fits. As shown in Fig. 1, it can be observed that the agreement between the fits of CTRW with ASY, TPL and FDE can better capture the non-Fickian behavior of solute transport in heterogeneous soil column, especially the tails of the BTCs, with respect to the ADE fits.

5 Conclusion

We used ADE and the general CTRW with TPL, ASY and FDE functions to characterize solute transport in the 1250cm saturated heterogeneous soil columns. The fits of CTRW with TPL, ASY and FDE functions better capture the non-Fickian transport in the heterogeneous long soil column, especially the tails of the BTCs. And to characterize the non-Fickian transport in such a heterogeneous soil column by using CTRW with a single-β-value’s FDE function and stable velocity value is recommendable.

 

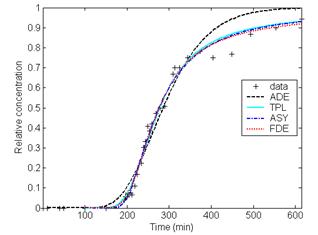
(a)

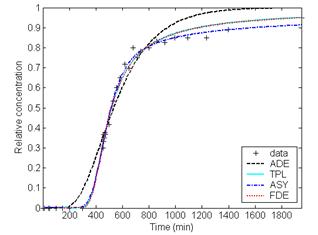
(b)

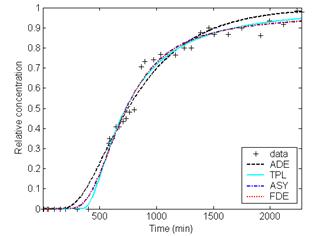
(c)

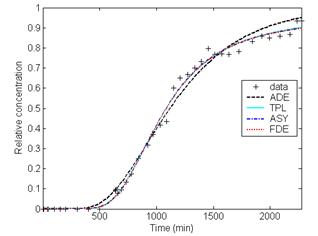
(d)

Fig.1 Comparison of the measured heterogeneous soil column concentrations with the fitting results of ADE and CTRW with ASY, TPL and FDE at distances (a) 300cm, (b) 600cm, (c) 800cm, and (d) 1000cm, respectively

 

Acknowledgments

This research was partly supported by the National Natural Science Foundation of China (grant number: 50479011). The authors acknowledge Prof. Renduo Zhang for offering the laboratory experimental data for heterogeneous soil columns.

References

[1]      Bear, J., 1972. Dynamics of fluids in porous media. American Elsevier Publishing Company, New York.

[2]      Benson D.A., 1998. The fractional advection-dispersion equation: development and application. Dissertation of Doctorial Degree, University of Nevada Reno.

[3]      Benson D.A., Wheatcraft S.W., Meerschaert, M. M., 2000a. Application of a fractional advection-dispersion equation, Water Resources Research, 36(6): 1403-1412.

[4]      Benson D. A., Wheatcraft S.W., and Meerschaert, M. M., 2000b. The fractional-order governing equation of Lévy motion. Water Resources Research, 36 (6): 1413-1423.

[5]      [5] Berkowitz, B. and H. Scher, 1995. On characterization of anomalous dispersion in porous and fractured media. Water Resources Research, 31 (6), 1461-1466.

[6]      Berkowitz, B. and H. Scher, 1997. Anomalous transport in random fracture networks. Physical Review Letters, 79 (20), 4038-4041.

[7]      Berkowitz, B. and H. Scher, 1998. Theory of anomalous chemical transport in fracture networks. Physical Review E, 57 (5), 5858-5869.

[8]      Berkowitz, B., H. Scher and S. E. Silliman, 2000. Anomalous transport in laboratory-scale, heterogeneous porous media. Water Resources Research, 36(1), 149-158 (Minor correction appears in Water Resources Research, 36(5), 1371, 2000).

[9]      Berkowitz, B., J. Klafter, and R. Metzler, 2002. Physical pictures of transport in heterogeneous media: advection-dispersion, random-walk, and fractional derivative formulations. Water Resources Research, 38 (10).

[10]  Bromly, M and C. Hinz, 2004. Non-Fickian transport in homogeneous unsaturated repacked sand. Water Resources Research, 40 (07402).

[11]  [11] Cortis, A., and B. Berkowitz, 2004. Anomalous transport in “classical” soil and sand columns. Soil Science Society of America Journal, 68, 1539-1548.

[12]  Cortis, A., C. Gallo, H. Scher and B. Berkowitz, 2004.Numerical simulation of non-Fickian transport in geological formations with multiple-scale heterogeneities. Water Resources Research, 40, W04209, doi: 10.1029/2003WR002750.

[13]  Cortis A., Y. Chen, H. Scher and B. Berkowitz, 2004.Quantitative characterization of pore scale disorder effects on transport in “homogeneous” granular media. Physical Review E, 70,041108.

[14]  Cortis, A. and B. Berkowitz, 2005. Computing “anomalous” contaminant transport in porous media: The CTRW Matlab toolbox, Ground Water, 43(6), 947-950.

[15]  Dentz, M., A. Cortis, H. Scher and B. Berkowitz, 2004. Time behavior of solute transport in heterogeneous media: Transition from anomalous to normal transport. Advances in Water Resources, 27(2), 155-173.

[16]  Garabedian, S. P., LeBlanc, D. R., Gelhar, L. W., Celia, M. A., 1991. Large-scale natural gradient tracer test in sand and gravel, Cape Cod, Massachusetts: 2. Analysis of spatial moments for a nonreactive tracer. Water Resources Research, 27 (5), 911 –924.

[17]  Huang Q. Z., and G. H. Huang, 2004. Modeling adsorbing solute transport with fractional advection dispersion equation. In Huang, G. and Pereira, L.S., 2004. Land and Water Management: Decision Tools and Practice, Proceedings of 2004 International Commission of Agricultural Engineering Conference, Beijing, China, Oct. 11-14, China Agricultural Press, 1046-1053.

[18]  Huang G., Huang, Q., Zhan, H., Chen, J., Xiong, Y., Feng, S., 2005. Modeling contaminant transport in homogeneous porous media with fractional advection-dispersion equation. Science in China, Ser. D Earth Sciences 48 (Suppl.II), 295-302.

[19]  Huang G. H., Q. Z. Huang, and H. B. Zhan, 2006.Evidence of one-dimensional scale-dependent fractional advection dispersion. Journal of Contaminant Hydrology, 85, 53-71.

[20]  Huang, K., N. Toride, and M. Th. van Genuchten, 1995. Experimental investigation of solute transport in large, homogeneous and heterogeneous, saturated soil columns. Transport in Porous Media, 20, 298–308.

[21]  Kosakowski, G., B. Berkowitz and H. Scher, 2001. Analysis of field observations of tracer transport in a fractured till. Journal of Contaminant Hydrology, 47(1), 29-51.

[22]  Levy, M. and B. Berkowitz, 2003. Measurement and analysis of non-Fickian dispersion in heterogeneous porous media. Journal of Contaminant Hydrology, 64 (3-4), 203-226.

[23]  Lu S., Molz F. J. and Fix G. J., 2002. Possible problems of scale dependency in applications of the three-dimensional fractional advection-dispersion equation to natural porous media. Water Resources Research, 38(9), 1165, doi: 10.1029/2001WR000624.

[24]  Margolin, G. and B. Berkowitz, 2002. Spatial behavior of anomalous transport. Physical Review E, 65, 031101.

[25]  Pachepsky Y., David B., and Walter R., 2000. Simulating Scale-Dependent Contaminant Transport in Soils with the Fractional Adevective-Dispersive Equation. Soil Science Society of America Journal, 64:1234-1243.

 

Table 1 Estimated values of parameters and normal of difference for TPL, ASY and FDE at different distances of the heterogeneous soil column