MA Hongyun, LU Wenxi, LI Jun

(Environment And Resource Academic, Jilin University, ChangChun Jilin 130026, China)

Abstract: The simulation period of the field soil water numerical model always lasts for a long period, such as a growth season of crop. On the other hand, the simulation face a problem of inferior stabilization, so we have to use minute volume to difference simulated time in order to make it stable. In allusion to the small rangeability of field soil water in most simulated times, a new method (phase-division-method) was generalized, and it was joined with iteration to lower the instability effect of two main factors (the step-size of time and the representation of water characteristic parameter). By this method, we can use day volume as step-size to run the numerical simulation, and make sure it works under stable and fast. Finally, a section of alfalfa growth season was taken as the investigated subject to test the model we established and the method we generalized. It was confirmed that the method is highly efficient.

Keywords: field soil water, numerical simulation, stabilization, iteration, phase-division-method

Introduction

The stabilization of numerical simulation is about error that may gradually increase in the process of simulating. And if the error becomes too large to make the result valuable, the simulation model will be recognized as instability under some given situation.

Soil water numerical simulation faced a problem of inferior stabilization， because there are a lots of factors work on instability and make the simulating complicated^[1]. The factors of instability can be generalized into four main aspects: 1. Soil water simulation equation. Different simulation equation have different stability, but most soil water model that we used today are based on Richards Continuity Equation; 2. Model solution. It included analytical method and numerical method. The result that

calculated by analytical method is precise and without instable problem, but it can only solve some simple questions. We generally solve practical questions by numerical method, which will cause error fated. Finite Difference which belongs to numerical method will be used in this paper; 3. Step-size of discretization. In any numerical simulation, step-size of time and space will directly affect the stability, accuracy and calculating rate. Step-size choice is to find equilibrium in them three. 4. Representation of parameters. The parameters (hydraulic conductivity and diffusivity) are variables which are functions of soil moisture in soil water simulation. A proper algorithm that used to calculate parameters can made it approach its real value better, so that the simulation stability will be insured.

Field soil water numerical simulation lasts for a relatively long period, generally it investigated at least a growth season of crop (120d to 180d) or more. However step-size of time is being restricted into minutes or seconds in order to make the simulating stable, because the simulation model has an inferior stabilization. That is to say simulation time will be divided into ten thousands phases or more, the simulation will last for a long time. To solve this problem, the authors introduce Phase-Division-Method, and integrate it with iteration algorithm. Then we can take 1day as step-size of time and make sure the accuracy of simulating results.

1 Numerical Simulation Model of Field Soil Water

In field, soil water mainly moved along vertical. In this paper, we build vertical one dimension soil water numerical model by continuity equation (A.Richads,1931), boundary and initial conditions.

1.1 Vertical one dimension soil water numerical model

We set soil surface as zero point and vertical downwards as positive axis to build one dimension coordinate system. The model can be expressed as following:

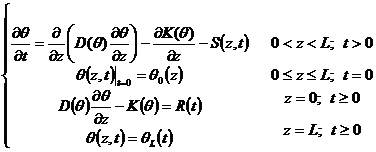（1）

Where is the volumetric water content （mm³/mm³）；is the concentration-dependent soil water diffusivity （mm²/d）；is the concentration-dependent hydraulic conductivity （mm/d）；z is depth below the soil surface (mm)；t is time （d）;is soil water uptake （d^-1）；L is the total depth （mm）；is evaporation intensity and precipitation infiltration intensity （evaporation is negative item and precipitation is positive item）（mm/d）。

1.2 The difference of the continuity equation

The differenced implicit expression of one dimension soil water continuity equation is as following 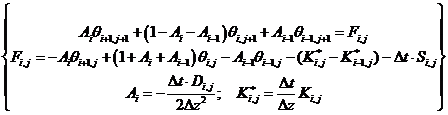^[2]:

（2）

Where the subscripts i refer to soil depths and j refer to times；is step-size of depth；is step-size of time.

1.3 The boundary treatment of the model

The boundary condition generally is part into three types. We are familiar with the first two type of them in soil water simulation, that is the first boundary type (water content of boundary is known) and the second boundary type (water flux of boundary is known).

For the first boundary type, we assume in equation （2）,（i=0 refer to above boundary；i=n+1 refer to nether boundary）. Where n is depth discretized number; is boundary water content.

For the second boundary type, we add into (above boundary) or (nether boundary) of equation (2). Where the sign of R is decided by flux direction, if water moves downwards, the sign of R is positive, otherwise negative.

1.4 Soil water uptake equation

Soil water uptake is the function of time, depth and water content. It can be expressed by the following experiential equation:

Where is soil water uptake validity equation (which shows how soil water content effects soil water uptake)；is root density distribution equation； is transpiration of crop under fully irrigated.^[3]

2 Factor Analysis and Treatment of Instability

To make sure that the simulating is stable, the factors that may cause instability are generalized into four items: a. step-size of time; b. the representation of discrete water content; c. the representation of parameters; d. step-size of depth.

In this four factors, step-size of depth sometimes is confine by test situation and accuracy of simulation. It can not be modulated freely. So we just suggest to making it bigger to benefit the stability of simulation if the accuracy is satisfactory. The representation of discrete water content will cause instability but trifling if it contrasts with effect of the representation of parameters, because the former is 1/50 to 1/1000 times smaller then the latter in quantitatively, the former effect is in the error band of the latter. So the main factors that produce errors are the representation of parameters and step-size of time.

At the following, iteration algorithm was used to eliminate the effect of parameters’ representation, and phase-division-method was used to dispel the effect that cause by time step-size.

2.1 Iteration algorithm be used to eliminate the effect of parameters’ representation

For the parameters is a function of water content, it is determined by the function expression (experiential equation) and soil water content. In the process of finite difference, originally continuous independent variable (water content) was discretized, the parameters be discretized at the same time. It is the point where the problem comes from, the problem is each moment of the whole phase time has different water content value. Then which water content value would be used to calculate the parameters, so that those parameters may approach the practical value better Is it the water content value of initial moment or of end moment or other moments The practices proved that the representation of parameters which be calculated by both water content of initial moment and end moment are inferior. So iteration algorithm is used to find the water content of right moment that can represent of the whole phase. Finally, the most representative water content is request to meet equation (5) or (6).

Hydraulic conductivity and diffusivity are calculated by Brooks-Corey model ^[4]:

（3）

（4）

Where is the most representative water content of phase i, is the moisture potential （mm），the subscript s is the value of saturated，b is constant defined by Brooks-Corey model.

Then to find more representative parameters is to find fitted. The following equation is commonly be used to calculate more representative water content.

（5）

（6）

Where is the water content of initial moment of j time phase；is water content of end moment of j time phase.

Process of iteration algorithm is: 1) assume as water content value of initial moment; 2) calculate parameters by equation (3) and (4); 3) calculate water content of the end moment; 4) calculate by equation (5); 5) iterate step 2 and 3; 6) evaluating error percentage of water content that calculated out last two times, if error percentage is unsatisfied then iterate step 4 and 5, otherwise finish calculation of this phase.

The flow of iteration algorithm is showed in fig.2, out of the broken line frame.

2.2 Phase-division-method was used to dispel the effect of time step-size

In field soil water numerical simulating, the rangeability of soil water content is very small except when precipitation or irrigation happened. Day volume as step-size to run the numerical simulation would be possible in most of phases. In some unstable phases, the error percentage may be too large to astringe. To solve this problem, phase-division-method was generalized, that is we divided a single phase whose error percentage is too large to astringe into n smaller phases to enhance its simulating stability. If the error percentage is still too large, we divided it once more until it gets convergence (see fig.1). We knew it from principium of numerical method that if only we discrete time tiny enough, we can always make the model simulated convergent by finite difference method.

2.3 Combination of iteration algorithm with phase-division-method

Iteration algorithm and phase-division-method are aimed at different factors to avoid instability. The combination of them two will be more efficient.

Iteration algorithm is familiar to us in numerical simulation, but if error is not being made by inefficient representation of parameters, iteration will get unsatisfied result or go into endless loop. A loop limit was set to solve this problem. When iteration reaches loop limit, this phase will be judged as instable phase, and phase-division-method cut-in to divide the phase into more tiny phases. Fig.2 shows simulation flow of linking iteration algorithm with phase-division-method.

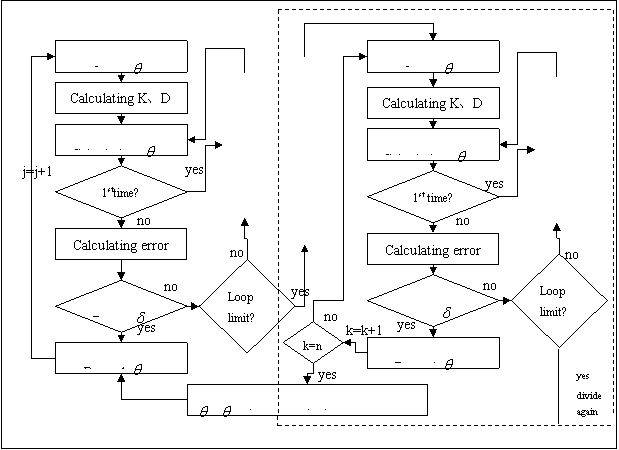
3 Simulation example

A section of alfalfa growth season was taken as the investigated subject to test the model we established and the method we generalized. Soil depth was assumed as 1m, step-size of depth set as 10cm; step-size of time set as 1day; initial total water content set as 325mm; crop root density introduced from reference [5]; simulation period set as 29^th June to 20^th August; irrigated 35mm and 32mm at 24^th July and 12^th August respectively.

When a phase is divided by phase-division-method, it was set to divide it into 10 equal length phases; a phase can be divided 5 times worst, that is a phase can small like 10^-5day if it need to be.

Simulation result see fig.3 and 4.

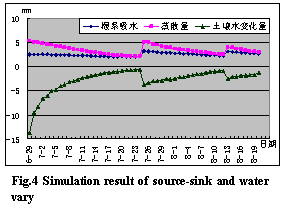Fig.3 shows total soil water content that changes with time and irrigation situation; Fig.4 shows soil water uptake, evapotranspiration (ET) and soil water variational quantity of different times. ET include soil water uptake and evaporation, and soil water variational quantity include ET, groundwater recharge and irrigation quantity.

The figures show that soil water uptake increased after irrigation, but smaller than ET; and then ET gradually approach soil water uptake. That is evaporation reaches its top after irrigation, and then gradually reduces. The nether boundary is drainage before 6^th July, for total soil water content is relatively big, presented in fig.4 as soil water variational quantity is bigger than ET in absolute value. After 6^th July, the nether boundary become supply boundary, fig.4 shows that soil water variational quantity is smaller than ET in absolute value.

Simulating phases only be divided for one times at 6.29, 7.24 and 8.12 respectively in the whole simulation processes. That is to say, the program finished 54days simulation by divided it into 81 phases. If we take 2 minutes as time step-size, phases will be 38880. The instability treatment we used is very efficient.