Groundwater Recharge with Its Ecology
RAINFALL INFILTRATION RECHARGE FUNCTION BUILDING WITH REGRESSION ANALYSIS WITH LYSIMETER DATA
QI Deng-hong
(Geological Environment
Monitoring Institute of Henan, Zhengzhou Henan,
450006, China)
Abstract: Accurately
calculating the quantity of rainfall infiltration recharge (RIR) to groundwater
is critical importance to the evaluation and management of groundwater
resources. Enormous works have been done to estimate the quantity of RIR and to
understand the processes of infiltration recharge by many methods including
field tests, lysimeters and etc. There are 35 lysimeters with 7 kind of soil
and 5 different depth (1m, 2m,3m, 5m and 7m) installed in
Zhengzhou Groundwater Balance Test Field to measure the infiltration recharge
flux and evaporation flux under conditions of fixed water tables at the bottoms
of the soil columns. A simple meteorological observation has built to measure
the rainfall, wind rate and water evaporation on ground surface. Some key infect
factors have been chosen to construct the rainfall infiltration recharge
functions (RIRF) for different kinds of soil after the relationship between the
RIR and rainfall and evaporation in the corresponding and former period by
uniform design method. Comparing the measured data with the calculated data by
RIRF, the small difference denotes that using the RIRF can calculate the RIR
more accurately than conventional method of product of rainfall and constant
RIR coefficient.
Key words: lysimeter;
regression analysis; rainfall infiltration recharge function (RIRF); uniform
design
1 Introduction
The process of
rainfall goes into groundwater through soil is called rainfall infiltration
process; the groundwater recharge is called rainfall
infiltration recharge (RIR). It is the main driving force of
surface contaminant polluting groundwater, and is also the main recharge source
of groundwater. Accurately calculating the quantity of RIR to
groundwater is critical importance to the evaluation and management of
groundwater resources. In the past groundwater estimation, groundwater
fluctuation data is often used to ascertain rainfall infiltration coefficient,
which is multiplied by rainfall to calculate RIR. In 70s and
80s of 20thcentury, many equilibrium experimental
points were built in China, where can use lysimeter observing RIR,
and calculating rainfall infiltration coefficient for evaluating the
groundwater resource[1,2].
Rainfall flux,
rainfall characters, lithologic characters of unsaturated zone, groundwater
depth, and human activities are the factors affect RIR, part of which
exist nonlinear relationship. Moreover, hysteresis and delayed reaction
occurred in rainfall infiltration[3-8]. So RIR is
a nonlinear function affected by many factors. But in the
past groundwater resource estimation, RIR is considered as a linear
function of rainfall (rainfall infiltration coefficient is a constant),
which has a big error to the facts, so it affects the accuracy of groundwater
resource evaluation.
Influencing factors
of RIR are selected through analyzing the observed data of
equilibrium experimental points in Zhengzhou and correlation
analysis. Rainfall infiltration function is established by using
regression analysis that studied the relationship between RIR and influencing
factors, which can analysis the rule of RIR.
2 Influencing
Factors Choosing
2.1Main
influencing factors
After rainfall
infiltration, calculating initial soil moisture distribution is a considerable
factor, because it determined the velocity of rainfall infiltration and soil
moisture storage in unsaturated zone, and can affect final infiltration
recharge. According to the soil moisture equilibrium principle, rainfall,
evaporation and infiltration recharge controlling mainly determine soil moisture
in unsaturated zone, and initial soil moisture is mainly affected by rainfall,
evaporation in a period of time before calculating. So regression model of
RIR is as follows:
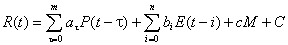 (1)
(1)
where, M is
groundwater depth[L];a、b、c、C are constant; m、n are prophase
rainfall, time length of water evaporation respectively, which can be evaluated
different values because of different influencing degree between rainfall and
evaporation. Using experiment-designing method can derive the reasonable value.
Because RIR decreasing as groundwater depth increasing when depth
exceed 1m,linear format is denoted for establishing unified model.
2.2 Establishing
model method and process
Regression model
consider evaporation and groundwater depth in different periods except
different periods of rainfall. Especially evaporation needs consideration,
because former evaporation will affect RIR. Usingtrial
method derives the numbers of former rainfall and evaporation in order to
get better result through less former rainfall and evaporation.
2.2.1 Uniform design abstract
The purpose
of uniform design is to derive satisfied parameters using least
experiments. Uniform design is a experiment designing method of
many factors and many levels which invented by two Chinsesemathematicians
named Fang Kaitai and Wang yuan, it is a scientific method of distributing
testing spots uniformly in experimental range, which can get reasonable result
especially for large range and many factors or levels of experiments[9].
Uniform design
often uses a uniform table Un(qs)and corresponding tables, U represents uniform
design; n represents numbers of experiments, q represents numbers of
levels; s is numbers of columns which can arrange numbers of s factors.
Every uniform design table is accompanied by a introduction table,
which explains degree of homogeneity of experiment.
The
steps of uniform design is as follows, 1)choosing reasonable factor and level based on
the purpose of experiment;2)listing the factors and their levels on the column and
the row according to the index of the number chosen from the chosen reasonable
uniform design table and use table.
2.2.2 Establishing model process
After the ranges of rainfall and evaporation and their experiment levels
have been determined, the test scheme is determined using uniform design
method. The average values of error square (AES) of every test are calculated.
The minimum ASE is determined by Krige method. The new test schemes with
miner interval near the column and row of minimum ASE are determined by uniform
design. The AES of new test schemes is calculated and the process repeats until
getting the most suitable number of former periods of rainfall and evaporation
that are used to regression analysis.
3 Rainfall
Infiltration Recharges Function
The
annual and monthly RIRFs of different soils are determined with this method.
3.1
Annual rainfall infiltration recharge model
Annual RIR has
little relationship with rainfall and evaporation in the former period and
evaporation in the corresponding period according to the former analysis. The
RIRF can be descried by the follow equation.
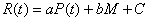 (2)
(2)
The coefficients
of equation 2 derived from measured data about rainfall, RIR and evaporation by
regress analysis method are listed in table 1. According to the regress
results, RIR is positive correlation with rainfall, but is negative correlation
with buried depth of groundwater level. The sensitivity of RIR to buried depth
of groundwater level is largest in silt from Xinxiang, and second in fine
sand from Kaifeng, and least in silt clay from Zhumadian shown that its
recharge mainly derived from preferential flow.
Table 1 Regression
coefficients of the annual RIR to rainfall and buried depth of groundwater
level in different soil lysimeters.
|
Regression coefficient |
a |
b |
C |
r |
F |
markedness |
|
Silty fine sand
from Kaifeng |
0.9171 |
-6.5041 |
-157.83 |
0.8124 |
84.43 |
markedly |
|
Loess-like sabulous clay
from Zhengzhou |
0.5026 |
-4.0071 |
-65.06 |
0.7097 |
44.15 |
markedly |
|
Light sabulous clay
from Xinxiang |
0.6200 |
-22.7100 |
-4.38 |
0.7539 |
57.27 |
markedly |
|
Mild clay from Zhumadian |
0.5522 |
-0.6881 |
-105.07 |
0.8398 |
104.05 |
markedly |
3.2 Monthly rainfall infiltration recharge function
The numbers of
former periods of rainfall and evaporation are both less than 10 according to
the former analysis, so 10 tests listed in table 2 are made under the directed
by uniform design. The corresponding determining coefficient, F value and ASE
are calculated respectively. Comparing the three characteristic values, the
best m and n are used to determine the
regression function and their regression coefficients are listed in table 3.
The coefficients of infiltration recharge functions show that the RIR is mainly
affected by the rainfall of two months before and the same month rainfall
counts for 58~ 67% of all rainfall. Monthly RIR is negative correlation to
monthly evaporation, especially the last past monthly because it evaporated
more water from soil in lysimeter, which may be led more water stay in soil
instead of recharging groundwater. When the buried depth of groundwater level
is more than 1m, the RIR decreases with the buried depth of groundwater
level. The decreasing rate is largest in loess loam, and it is decreasing in
loam, light loam, loan with silt interbed and fine sand. But the inverse
phenomena occur in loam from Zhumadian, which may be led by the ruleless macro
pores or cracks and strong preferential flow in the lysimeters.
Table 2 The test
scheme for monthly RIRF
|
Number of test |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
n |
7 |
3 |
10 |
6 |
2 |
9 |
5 |
1 |
8 |
4 |
Table3
Coefficients of monthly RIRFs
|
lithology |
Silty fine sand fromKaifeng |
Sabulous clay with thin clay
interbed fromAnyang |
Loess-like sabulous clay
fromZhengzhou |
Light sabulous clay
fromXinxiang |
Sabulous clay from Xuchang |
Mild clay from Nanyang |
Mild clay from Zhumadian |
|
Pt |
0.5065 |
0.1021 |
0.3025 |
0.2590 |
0.2568 |
0.2753 |
0.3212 |
|
Pt-1 |
0.2773 |
0.0388 |
0.0907 |
0.1067 |
0.1343 |
0.1420 |
0.1022 |
|
Pt-2 |
0.0193 |
0.0111 |
0.0637 |
0.0797 |
|
|
0.0598 |
|
Et |
-0.0234 |
-0.0044 |
-0.0016 |
-0.0128 |
-0.0489 |
-0.0175 |
-0.0143 |
|
Et-1 |
-0.0809 |
-0.0241 |
-0.0630 |
-0.0608 |
|
-0.0707 |
-0.0452 |
|
m |
-0.4980 |
-0.6592 |
-2.6799 |
-1.5224 |
-1.9956 |
-0.7241 |
0.2568 |
|
C |
15.7580 |
7.4900 |
20.4760 |
19.9150 |
16.0940 |
8.0648 |
2.3156 |
|
r |
0.8198 |
0.5681 |
0.7434 |
0.6956 |
0.7146 |
0.7970 |
0.8943 |
|
F |
96.69 |
22.48 |
58.26 |
44.20 |
28.70 |
100.65 |
188.33 |
Fig.1 shows that
the difference between monthly recharge data measured with calculated by
regression function, which shows the monthly RIRF constructed by regression
analysis can be used to calculate the RIR.
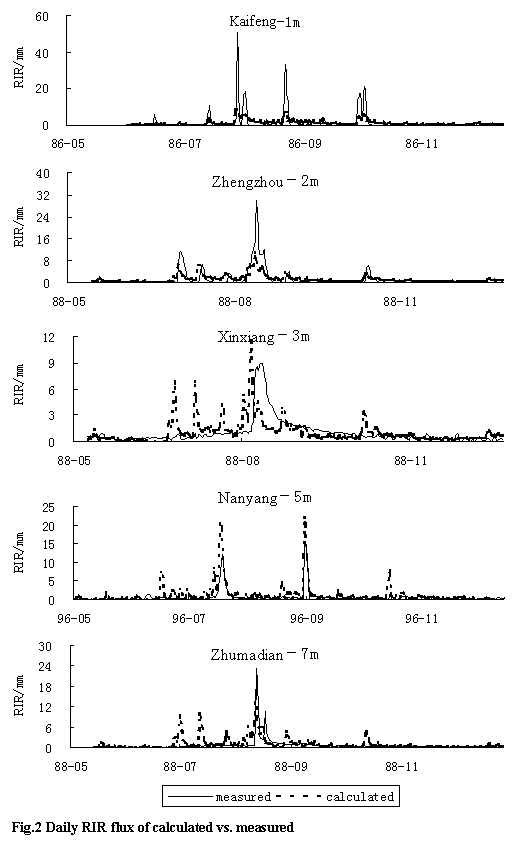
3.3 Daily rainfall
infiltration recharge function
The values of m
and n are less than 120 days i.e. 2 months according to the monthly RIRF. 24
tests with an interval of 5 days were taken under the direction of uniform
design, and their determining coefficient, F value and ASE are calculated
respectively. With the same method above, the best m and n are
used to determine the regression function and their regression coefficients are
listed in table 4. Fig.2 shows that the difference between the measured data
and calculated data by daily RIRF is large, especially of shallow buried depth
of groundwater table, which may be led by the non-linear correlation between
RIR and buried depth of groundwater table, and the delay of infiltration
recharge make the dairy RIR is little correlation to the daily rainfall.
4 Conclusions
The RIRFs with
different time scale are established by regression analysis with rainfall and
evaporation in same or/and former periods. Among the functions, annual and
monthly infiltration recharge function is well to calculate the recharge. RIR
is positive correlation with rainfall, but is negative correlation with buried
depth of groundwater level. The sensitivity of RIR to buried depth of
groundwater level is largest in silt fromXinxiang, and second in fine sand
from Kaifeng, and least in loam from Zhumadian shown that its recharge
mainly derived from preferential flow. For monthly scale, RIR is mainly
affected by the rainfall of two months before and the rainfall in the same
month counts for 58~67% of all rainfall. The daily RIRF is less accurate
because of the delay of infiltration and the irregular temporal distribution of
rainfall.
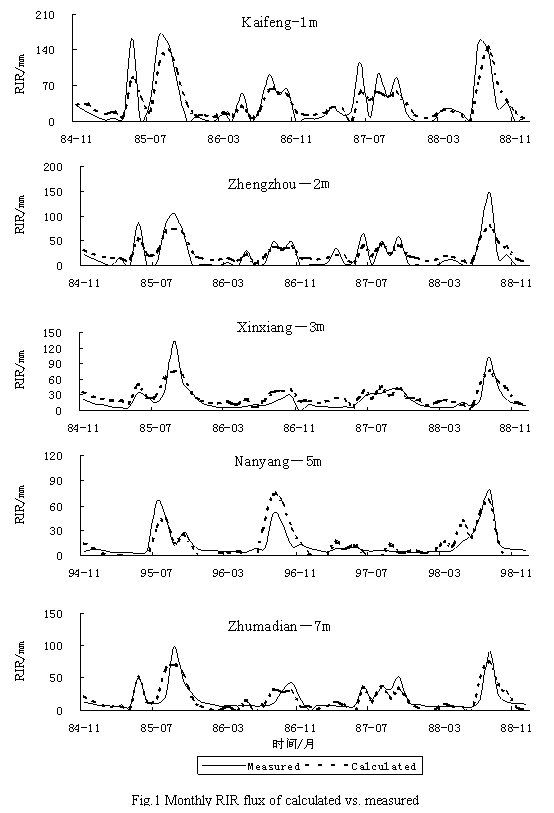
Table 4 Statistical characteristics of error of daily RIRF
|
lithology |
Buried depth of groundwater level |
1m |
2m |
3m |
5m |
7m |
合计 |
|
Silty fine sand fromKaifeng |
Minimum |
-70.36 |
-31.27 |
-31.07 |
-14.76 |
-6.73 |
-70.36 |
|
Maximum |
9.03 |
13.63 |
16.37 |
13.97 |
13.60 |
16.37 |
|
|
Average |
-0.10 |
0.21 |
-0.08 |
-0.06 |
0.03 |
0.00 |
|
|
Standard deviation |
5.09 |
2.30 |
2.37 |
1.96 |
1.97 |
2.99 |
|
|
Summary of square error |
129.61 |
26.56 |
28.02 |
19.30 |
19.47 |
44.59 |
|
|
Sabulous clay with thin clay
interbed from Anyang |
Minimum |
-45.15 |
-27.90 |
-8.44 |
-2.04 |
-1.54 |
-45.15 |
|
Maximum |
3.80 |
6.92 |
9.96 |
9.39 |
9.61 |
9.96 |
|
|
Average |
-0.15 |
0.09 |
0.14 |
-0.04 |
-0.03 |
0.00 |
|
|
Standard deviation |
2.66 |
1.51 |
0.88 |
0.82 |
0.81 |
1.52 |
|
|
Summary of square error |
35.57 |
11.39 |
3.92 |
3.39 |
3.26 |
11.50 |
|
|
Loess-like sabulous clay
fromZhengzhou |
Minimum |
-42.43 |
-22.34 |
-7.77 |
-4.72 |
-3.02 |
-42.43 |
|
Maximum |
5.36 |
7.49 |
11.69 |
11.59 |
11.69 |
11.69 |
|
|
Average |
-0.21 |
0.07 |
0.23 |
0.02 |
-0.10 |
0.00 |
|
|
Standard deviation |
3.58 |
1.82 |
1.30 |
1.28 |
1.28 |
2.06 |
|
|
Summary of square error |
64.11 |
16.59 |
8.71 |
8.23 |
8.19 |
21.17 |
|
|
Light sabulous clay
from Xinxiang |
Minimum |
-42.57 |
-22.37 |
-7.58 |
-4.75 |
-3.04 |
-42.57 |
|
Maximum |
5.35 |
7.50 |
11.55 |
11.45 |
11.55 |
11.55 |
|
|
Average |
-0.21 |
0.07 |
0.23 |
0.02 |
-0.10 |
0.00 |
|
|
Standard deviation |
3.58 |
1.82 |
1.30 |
1.28 |
1.28 |
2.06 |
|
|
Summary of square error |
64.22 |
16.60 |
8.65 |
8.20 |
8.19 |
21.17 |
|
|
Sabulous clay from Xuchang |
Minimum |
-45.35 |
-18.27 |
-5.96 |
-3.89 |
-1.31 |
-45.35 |
|
Maximum |
4.58 |
9.63 |
13.07 |
12.59 |
12.69 |
13.07 |
|
|
Average |
-0.20 |
0.11 |
0.20 |
-0.10 |
-0.02 |
0.00 |
|
|
Standard deviation |
3.68 |
1.73 |
1.28 |
1.19 |
1.20 |
2.05 |
|
|
Summary of square error |
67.74 |
15.00 |
8.41 |
7.12 |
7.21 |
21.09 |
|
|
Mild clay from Nanyang |
Minimum |
-42.87 |
-15.44 |
-22.88 |
-30.91 |
-41.61 |
-42.87 |
|
Maximum |
7.45 |
16.62 |
14.02 |
16.47 |
16.33 |
16.62 |
|
|
Average |
-0.17 |
0.14 |
0.09 |
-0.02 |
-0.04 |
0.00 |
|
|
Standard deviation |
2.66 |
1.40 |
1.42 |
1.62 |
1.83 |
1.85 |
|
|
Summary of square error |
35.59 |
9.89 |
10.10 |
13.12 |
16.78 |
17.09 |
|
|
Mild clay from Zhumadian |
Minimum |
-27.49 |
-27.64 |
-27.77 |
-21.02 |
-21.73 |
-27.77 |
|
Maximum |
8.80 |
11.09 |
12.77 |
15.77 |
15.81 |
15.81 |
|
|
Average |
-0.01 |
-0.02 |
0.04 |
0.01 |
-0.02 |
0.00 |
|
|
Standard deviation |
2.11 |
1.82 |
1.71 |
1.57 |
1.71 |
1.79 |
|
|
Summary of square error |
22.18 |
16.64 |
14.55 |
12.28 |
14.56 |
16.04 |
References
1. Wang, D., Zhang,
R., Shi, Y., et al., 1995. Foundation of Hydrogeology. Geology
Press, Beijing.
2. Xu, H., 2001.
Exploitation and protection of water resources. Geology Press, Beijing.
3. Zhang, P., Li, R.,
1999. The Affecting Factors of Underground Water Supplied by Rain Penetration,
Journal of Liaoning University, 26(2):118-122.
4. Wu, J., Zheng, J.,
1999. Model Estimation of Sub-coefficient of Recharge by Rainfall Infiltration,
Journal of Hohai University, 27(6):7-11.
5. Wang, Z., Li, Sh.,
Xin, X.,et al.,1998. System analysis of precipitation delay recharge, Survey
Science and Technology, 4:11-14.
6. Li, Y., 1997.
Lagging distribution of precipitation recharge to phreatic water, Survey
Science and Technology, 3:22-26.
7. Chen Ch.,
1998. The weight function method of hysteresis recharge- a method to deal with
lagging of precipitation recharge to phreatic water, Hydrogeology and
Engineering geology, 6:22-24.
8. Zhou, M., Jin, M.,
Wei, Xiu, et al, 2002. Analysis of precipitation recharge using observed data
of lysimeter, Geological Science and Technology Information, 21(1):37-40.




