Evolutional Rules of Regional Groundwater System
WELL FUNCTION APPROXIMATION OF CONFINED AQUIFERS AND ITS APPLICATION IN THE ORDOS BASIN
Yin Lihea Zhang Maoshengb Hou Guangcaib,c Wang Xiaoyongb
a China University of Geosciences(Beijing),
b Xi’an Institute of Geology and Mineral Resources,
cShoole of Resources and
Environment of the
Abstract: Some approximation of Theis solution for confined aquifers are reviewed and compared. The most accurate approximation of the well function, based on the accurate comparison, was applied to the hydrogeogical parameters determination using least-square method.
Introduction
Pumping tests are commonly used to determine the transmissivity and storage coefficients of a confined aquifer. Computation of the Theis’ well function (1935) is an essential part of this process. Most early investigations involved reading the value of the well function from a table, using an approximation valid for small values of the argument or using numerical integration. Practical well function approximation was widely studied, Allen (1954) and Hastings (1955) presented standard approximations for the exponential integral. Recently, approximations of the well function valid for the entire range of the argument were proposed for both confined and leaky aquifers (Swamee and Ojha 1990a; Swamee and Ojha 1990b). Srivastava (1995,1998) assessed computation time and accuracy of various well function approximations based on the slope matching techniques (Srivastava 1994). Tseng and Lee(1998) presented a thorough discussion on approximations to the Theis well function. Most recently, Barry(2000) put forward the full range well function approximation formula and Pham(2003)revisited the well function approximation and presented an easy graphical curve matching technique for Theis’ solution.
Well Function Approximation for Confined Aquifers
An analytical expression for the drawdown in an observation well located at a distance r from the pumping well, assuming a homogeneous and isotropic aquifer with a uniform thickness and infinite in areal extent, was presented by Theis (1935).
![]() (1)
(1)
where s=drawdown; Q=constant pumping rate; and T=transmissivity. The dimensionless parameter u, which depends on time t, is defined as
![]() (2)
(2)
where S= storage coefficient; and W(u)= the well function defined by an infinite series as
![]() (3)
(3)
Since the well function is an integral function of S and T, it is not possible to determine explicitly the aquifer parameters S and T from a set of values of s and t at an observation well. For practical purposes, the simplest was proposed by Cooper and Jocob(1946) for u<0.05, thus
W(u)=-0.5772-lnu (4)
Allen(1954) and Hastings(1955) obtained nearly exact approximations for the well function as follows:
For u≤1时,W(u)=-lnu+a0+a1u+a2u2+a3u3+a4u4+a5u5 (5a)
For u≥1时,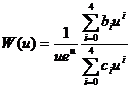 (5b)
(5b)
Where the rounded-off values of the constants are giver by
a0=-0.57722; a1=0.99999; a2=-0.24991; a3=0.05519; a4=-0.00976; a5=0.00108
b0=0.2677; b1=8.63467; b2=18.05902; b3=8.57333; b4=1;
c0=3.95850;c1=21.09965; c2=25.63296; c3=9.57332; c4=1
the error is Equation 5a is less than 2×10-7,and that in equation 4b is less than 2×10-8 exp(-u)/u(Abramowitz and stegun 1970). Swamee and Ojha(1990a)proposed approximations for the well function valid in the full range.
 (6)
(6)
Srivastava (1995) concluded that approximate expression given by (6) is less accurate and more computationally intensive than those given in (5). Srivastava (1998), based on the Slope-matching technique, proposed the more accuracy and less computationally intensive approximations, given by the following:
For u≤1时,![]() (7a)
(7a)
For u≥1时,![]() (7b)
(7b)
Where C1 is Euler’s constant, i.e. C1=exp(-0.5772)。Peng-Hsiang Tseng (1998) presented a well function approximation for u>1:
![]() (8)
(8)
where N=number of quadrature points; yi=root of the Laguerre polynomials; and ai=Laguerre coefficients.
Srivastava recently presented a approximation with accuracy less than ±0.00511% (personal communication).
![]() (9)
(9)
Where ![]()
A comparative estimation of well function was carried out in this study based on Equations 3 through 9, for u from 0.0001 to 10, as shown in Figure 1 and appendix 1, respectively. The following conclusions are drawn: (1)the first five-term, the first ten-term, the first twenty-term and the first forty-term can approximate well for u<1,u<3、u<5 and u<8 respectively. The first fifty-term produces the same value as terms more than fifty, which can be regarded as the standard value of the well function. (2) Copper and Jacob’s approximation works for u<0.1 (3) approximations in equation 5, 6, 7 and 8 are accurate for u up to 8 (4) more precisely, the equation 5 obtained the large error, while the other produced errors less than 0.01.
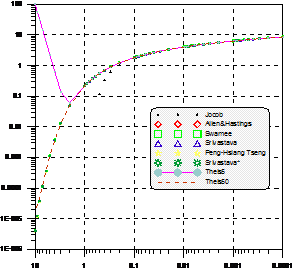
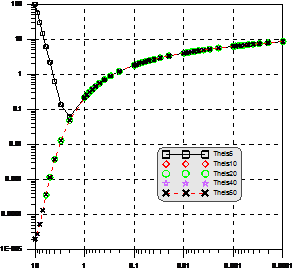
Application of Least-square method to hydrogeological parameters determinati- on
Various methods are available for calculation hydrogeogical parameters. The most common ones are type-curve method and the Jocob linear interpretation. Other methods are also described in literatures, such as curve-matching scheme (Li 1993), statistical analyses (Li 2004) and EXCRL macro programming (Keith 2002). Based on the study on the well function approximation, a least-square based method is applied to the parameters determination. Substituting 7a and 2 into 1 gives:
![]() (10)
(10)
![]() (11)
(11)
其中![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Pumping test data from B13 in the Ordos basin is used to calculate hydrogeological parameters, listing in the table 1.
Tatle1 pluming test data
|
Time(Min) |
drawdown |
|
Time(Min) |
drawdown |
|
1 |
12.29 |
|
80 |
24.41 |
|
2 |
17.49 |
|
100 |
24.73 |
|
3 |
15.44 |
|
150 |
25.54 |
|
4 |
16.54 |
|
180 |
25.53 |
|
6 |
17.61 |
|
270 |
25.79 |
|
8 |
18.79 |
|
360 |
26.05 |
|
10 |
21.61 |
|
450 |
26.26 |
|
20 |
24.09 |
|
540 |
26.41 |
|
30 |
23.22 |
|
630 |
26.56 |
|
40 |
23.44 |
|
720 |
26.68 |
|
50 |
23.82 |
|
810 |
26.82 |
|
60 |
24.08 |
|
900 |
26.89 |
The fitting equation is as follow and the water level match curve has a good agreement between observed and calculated values.
![]() (12)
(12)
Fitting coefficient is used to calculate the T value. Comparing to the T obtained form Jocob linear fitting (55.6 m2/d), the T value by least-square is 49.9m2/d. this indicates that in practical the least-square is a feasible way to calculate hydrogeological parameters.
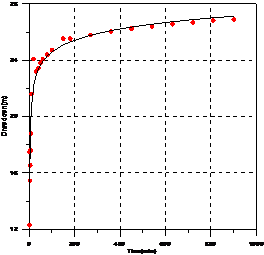
Results and Discussion
Base on the study, the following remarks are drawn:
1. The most optimum well function approximation suitable for computer-aided calculation is put forward, based on the comparative study on various well function approximations.
2. Determination of hydrogeological parameters using least-square method can be realized by programming or by software, such as DSP、SPSS or MATLAB.
3. Determination of hydrogeological parameters using least-square method can reduce error caused by artificial matching method.
Acknowledgments
This work was supported by Groundwater Investigation in the Ordos Basin Project. The writers wish to express their sincere thanks to Mr. Rajesh Srivastava and Dr. Pham Huy Giao for providing his papers on the well function approximation.
References
[1] Abramowitz, M., and I.A. Stegun. 1970. Handbook of
Mathematical Functions.
[2] Allen,E.E. 1954. Analytical approximations. Math. Tables Aids Comp. 8 No. 55:162-164
[3]
[4] Barry,D.A., Parlarge J.-Y., and Li L., approximation for the exponential integral(Theis well function),Journal of Htdrology 227, 287-291
[5] Cooper, H.H. Jr.. and C.E.Jocob 1946. A generalized graphical method for evaluation formation constants and summarizing well-field history, Transactions. American Geophysical Union 27. 526-534
[6] Giao,P.H.,2003. Revisit of well function approximation and an easy graphical curve matching technique for theis’ solution, Ground Water 41,no. 3: 387-390
[7] Keith J. Halford and Eve L. Kuniansky, Documentation of spreadsheets for analysis of aquifer-test and slug-test data, U.S. Geological Survey open-file report 02-197
[8] Li,C.Q.,Zhu,G.r., and Jiang S.M., 2004, application of statistical analyses to a solution to the Theis’s model, Hydrogeology and engineering geology, 2004(2), 75-78
[9] Li,J.j., 1993.curve-matching method for obtaining the n-th average water–table drop rate in determining hydrogeological parameters, Shangdong Geology, 1993(9),94-102
[10] Swamee, P.K.,and Ojha, C.S.P.,1990a. Pump test analysis of confined aquifer. J. Irrig. And Drain. Engre/, ASCE, 116(1),66-106
[11] Swamee, P.K.,and Ojha, C.S.P.,1990b. Pump test analysis of leaky aquifer. J. Irrig. And Drain. Engineering, ASCE, 116(5),645-655
[12] Srivastava, R.,1995, Implications of using approximate expressions for well function. J. Irrig. And Drain. Engineering. 121. no. 6: 459-462
[13] Srivastava, R., and A. Guzman-Guzman. 1994. Analysis of slope-matching methods for aquifer parameter determination. Ground Water 32,no. 4: 470-475
[14] Srivastava, R., and A. Guzman-Guzman.1998. Practical approximations of the well function, Ground Water 36,no. 5: 844-848
[15] Theis,C.V.(1935). “The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage.” Trans., Am. Geophys. Union, 16(Ⅱ), 519-524
[16] Tseng,P.H.,and Lee, T.C.,1998. Numerical evaluation of exponential integral: Theis well function approximation. J. Hydrlo., 205,38-51
Appendix 1: Estimation of well function
|
u |
W(u) |
|
|
|
|
| |||||
|
Jocab |
Allen& |
Swamee |
Srivastava |
Peng- Hsiang Tseng |
Srivastava* |
Thesis(5) |
Thesis(10) |
Thesis(20) |
Thesis(40) |
Thesis(50) | |
|
0.0001 |
8.633140 |
8.633240 |
8.651972 |
8.633237 |
|
8.633153 |
8.633240 |
8.633240 |
8.633240 |
8.633240 |
8.633240 |
|
0.0002 |
7.939993 |
7.940193 |
7.956879 |
7.940186 |
|
7.940064 |
7.940193 |
7.940193 |
7.940193 |
7.940193 |
7.940193 |
|
0.0003 |
7.534528 |
7.534828 |
7.550393 |
7.534818 |
|
7.534667 |
7.534828 |
7.534828 |
7.534828 |
7.534828 |
7.534828 |
|
0.0004 |
7.246846 |
7.247246 |
7.262062 |
7.247232 |
|
7.247060 |
7.247246 |
7.247246 |
7.247246 |
7.247246 |
7.247246 |
|
0.0005 |
7.023702 |
7.024202 |
7.038472 |
7.024185 |
|
7.023995 |
7.024202 |
7.024202 |
7.024202 |
7.024202 |
7.024202 |
|
0.0006 |
6.841381 |
6.841981 |
6.855829 |
6.841960 |
|
6.841757 |
6.841981 |
6.841981 |
6.841981 |
6.841981 |
6.841981 |
|
0.0007 |
6.687230 |
6.687930 |
6.701443 |
6.687906 |
|
6.687691 |
6.687930 |
6.687930 |
6.687930 |
6.687930 |
6.687930 |
|
0.0008 |
6.553699 |
6.554499 |
6.567738 |
6.554471 |
|
6.554248 |
6.554499 |
6.554499 |
6.554499 |
6.554499 |
6.554499 |
|
0.0009 |
6.435916 |
6.436816 |
6.449830 |
6.436784 |
|
6.436555 |
6.436816 |
6.436816 |
6.436816 |
6.436816 |
6.436816 |
|
0.0010 |
6.330555 |
6.331555 |
6.344380 |
6.331520 |
|
6.331286 |
6.331555 |
6.331555 |
6.331555 |
6.331555 |
6.331555 |
|
0.0020 |
5.637408 |
5.639407 |
5.651379 |
5.639338 |
|
5.639108 |
5.639407 |
5.639407 |
5.639407 |
5.639407 |
5.639407 |
|
0.0030 |
5.231943 |
5.234941 |
5.246818 |
5.234837 |
|
5.234663 |
5.234941 |
5.234941 |
5.234941 |
5.234941 |
5.234941 |
|
0.0040 |
4.944261 |
4.948257 |
4.960290 |
4.948119 |
|
4.948018 |
4.948257 |
4.948257 |
4.948257 |
4.948257 |
4.948257 |
|
0.0050 |
4.721117 |
4.726111 |
4.738396 |
4.725940 |
|
4.725918 |
4.726111 |
4.726111 |
4.726111 |
4.726111 |
4.726111 |
|
0.0060 |
4.538796 |
4.544787 |
4.557354 |
4.544582 |
|
4.544639 |
4.544787 |
4.544787 |
4.544787 |
4.544787 |
4.544787 |
|
0.0070 |
4.384645 |
4.391633 |
4.404483 |
4.391394 |
|
4.391530 |
4.391633 |
4.391633 |
4.391633 |
4.391633 |
4.391633 |
|
0.0080 |
4.251114 |
4.259098 |
4.272214 |
4.258825 |
|
4.259035 |
4.259098 |
4.259098 |
4.259098 |
4.259098 |
4.259098 |
|
0.0090 |
4.133331 |
4.142310 |
4.155668 |
4.142005 |
|
4.142285 |
4.142310 |
4.142310 |
4.142310 |
4.142310 |
4.142310 |
|
0.0100 |
4.027970 |
4.037945 |
4.051515 |
4.037606 |
|
4.037952 |
4.037945 |
4.037945 |
4.037945 |
4.037945 |
4.037945 |
|
0.0200 |
3.334823 |
3.354723 |
3.368824 |
3.354061 |
|
3.354871 |
3.354723 |
3.354723 |
3.354723 |
3.354723 |
3.354723 |
|
0.0300 |
2.929358 |
2.959134 |
2.971913 |
2.958165 |
|
2.959255 |
2.959134 |
2.959134 |
2.959134 |
2.959134 |
2.959134 |
|
0.0400 |
2.641676 |
2.681279 |
2.692115 |
2.680017 |
|
2.681335 |
2.681279 |
2.681279 |
2.681279 |
2.681279 |
2.681279 |
|
0.0500 |
2.418532 |
2.467914 |
2.476824 |
2.466375 |
|
2.467909 |
2.467914 |
2.467914 |
2.467914 |
2.467914 |
2.467914 |
|
0.0600 |
2.236211 |
2.295322 |
2.302600 |
2.293520 |
|
2.295272 |
2.295323 |
2.295323 |
2.295323 |
2.295323 |
2.295323 |
|
0.0700 |
2.082060 |
2.150853 |
2.156883 |
2.148803 |
|
2.150773 |
2.150854 |
2.150854 |
2.150854 |
2.150854 |
2.150854 |
|
0.08 |
1.948529 |
2.026956 |
2.032118 |
2.024671 |
|
2.026858 |
2.026957 |
2.026957 |
2.026957 |
2.026957 |
2.026957 |
|
0.09 |
1.830746 |
1.918760 |
1.923392 |
1.916254 |
|
1.918654 |
1.918760 |
1.918760 |
1.918760 |
1.918760 |
1.918760 |
|
0.10 |
1.725385 |
1.822939 |
1.827322 |
1.820225 |
|
1.822832 |
1.822940 |
1.822940 |
1.822940 |
1.822940 |
1.822940 |
|
0.20 |
1.032238 |
1.222666 |
1.229405 |
1.218538 |
|
1.222643 |
1.222666 |
1.222666 |
1.222666 |
1.222666 |
1.222666 |
|
0.30 |
0.626773 |
0.905692 |
0.911168 |
0.901153 |
|
0.905710 |
0.905692 |
0.905692 |
0.905692 |
0.905692 |
0.905692 |
|
0.40 |
0.339091 |
0.702394 |
0.704052 |
0.698171 |
|
0.702415 |
0.702397 |
0.702396 |
0.702396 |
0.702396 |
0.702396 |
|
0.50 |
0.115947 |
0.559787 |
0.558469 |
0.556347 |
|
0.559799 |
0.559793 |
0.559789 |
0.559789 |
0.559789 |
0.559789 |
|
0.60 |
-0.066374 |
0.454392 |
0.451550 |
0.451966 |
|
0.454395 |
0.454405 |
0.454395 |
0.454395 |
0.454395 |
0.454395 |
|
0.70 |
-0.220525 |
0.373780 |
0.370419 |
0.372375 |
|
0.373777 |
0.373810 |
0.373785 |
0.373785 |
0.373785 |
0.373785 |
|
0.80 |
-0.354056 |
0.310607 |
0.307264 |
0.310024 |
|
0.310601 |
0.310667 |
0.310612 |
0.310612 |
0.310612 |
0.310612 |
|
0.90 |
-0.471839 |
0.260192 |
0.257111 |
0.260041 |
|
0.260185 |
0.260310 |
0.260200 |
0.260200 |
0.260200 |
0.260200 |
|
1.00 |
-0.577200 |
0.219390 |
0.216658 |
0.219100 |
0.209314 |
0.219384 |
0.219606 |
0.219400 |
0.219400 |
0.219400 |
0.219400 |
|
2.00 |
-1.270347 |
0.048900 |
0.048352 |
0.048636 |
0.047920 |
0.048901 |
0.060764 |
0.048912 |
0.048916 |
0.048916 |
0.048916 |
|
3.00 |
-1.675812 |
0.013048 |
0.012927 |
0.013019 |
0.012821 |
0.013049 |
0.135438 |
0.012737 |
0.013064 |
0.013064 |
0.013064 |
|
4.00 |
-1.963494 |
0.003779 |
0.003747 |
0.003779 |
0.003707 |
0.003780 |
0.632061 |
-0.003492 |
0.003795 |
0.003795 |
0.003795 |
|
5.00 |
-2.186638 |
0.001148 |
0.001139 |
0.001150 |
0.001122 |
0.001148 |
2.205723 |
-0.078845 |
0.001164 |
0.001164 |
0.001164 |
|
6.00 |
-2.368959 |
0.000360 |
0.000357 |
0.000361 |
0.000351 |
0.000360 |
6.091041 |
-0.561980 |
0.000360 |
0.000376 |
0.000376 |
|
7.00 |
-2.523110 |
0.000115 |
0.000114 |
0.000116 |
0.000112 |
0.000115 |
14.283695 |
-2.907132 |
-0.000267 |
0.000131 |
0.000131 |
|
8.00 |
-2.656642 |
0.000038 |
0.000037 |
0.000038 |
0.000036 |
0.000038 |
29.734470 |
-12.009620 |
-0.006310 |
0.000053 |
0.000053 |
|
9.00 |
-2.774425 |
0.000012 |
0.000012 |
0.000012 |
0.000012 |
0.000012 |
56.546825 |
-41.814825 |
-0.073066 |
0.000027 |
0.000028 |
|
10.00 |
-2.879785 |
0.000004 |
0.000004 |
0.000004 |
0.000004 |
0.000004 |
100.175770 |
-127.259597 |
-0.647426 |
-0.000010 |
0.000020 |




